
【题目】△ABC中,BC=12,高AD=8,矩形EFGH的一边GH在BC上,顶点E、F分别在AB、AC上,AD与EF交于点M.
(1)求证:![]() ;
;
(2)设EF=x,EH=y,写出y与x之间的函数表达式;
(3)设矩形EFGH的面积为S,求S与x之间的函数表达式,并写出S的最大值.

【答案】(1)见解析;(2)y=8﹣![]() x(0<x<12);(3)S矩形EFGH=﹣
x(0<x<12);(3)S矩形EFGH=﹣![]() (x﹣6)2+24,Smax=24.
(x﹣6)2+24,Smax=24.
【解析】
(1)先判断出AM是△AEF的高,再判断出△AEF∽△ABC,即可得出结论;(2)先判断出四边形EMDG是矩形,得出DM=EH,进而表示出AM=8﹣y,借助(1)的结论即可得出结论;(3)由矩形的面积公式得出函数关系式,即可得出结论.
解:(1)∵四边形EFGH是矩形,
∴EF∥BC,
∵AD是△ABC的高,
∴AD⊥BC,
∴AM⊥EF,
∵EF∥BC,
∴△AEF∽△ABC,
∴![]() (相似三角形的对应边上高的比等于相似比);
(相似三角形的对应边上高的比等于相似比);
(2)∵四边形EFGH是矩形,
∴∠FEH=∠EHG=90°,
∵AD⊥BC,
∴∠HDM=90°=∠FEH=∠EHG,
∴四边形EMDH是矩形,
∴DM=EH,
∵EF=x,EH=y,AD=8,
∴AM=AD﹣DM=AD﹣EH=8﹣y,
由(1)知,![]() ,
,
∴![]() ,
,
∴y=8﹣![]() x(0<x<12);
x(0<x<12);
(3)由(2)知,y=8﹣![]() x,
x,
∴S=S矩形EFGH=xy=x(8﹣![]() x)=﹣
x)=﹣![]() (x﹣6)2+24,
(x﹣6)2+24,
∵a=﹣![]() <0,
<0,
∴当x=6时,Smax=24.


科目:初中数学 来源: 题型:
【题目】小红家的阳台上放置了一个晒衣架如图①.图②是晒衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点立于地面.经测量:AB=CD=136 cm,OA=OC=51 cm,OE=OF=34 cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32 cm.垂挂在衣架上的连衣裙总长度小于________cm时,连衣裙才不会拖落到地面上.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,⊙O与⊙P相交于A、B两点,点P在⊙O上,⊙O的弦AC切⊙P于点A,CP及其延长线交⊙P于D、E,过点E作EF⊥CE交CB的延长线于F.
(1)求证:BC是⊙P的切线;
(2)若CD=2,CB=2![]() ,求EF的长.
,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y=mx2+(m﹣2)x﹣2m+2(m≠0).
(1)求证:抛物线与x轴有交点;
(2)若抛物线与x轴交于点A(x1,0),B(x2,0),点A在点B的右侧,且x1+2x2=1.
①求m的值;
②点P在抛物线上,点G(n,﹣![]() n﹣
n﹣![]() ),求PG的最小值.
),求PG的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b<0;②abc<0;③b2﹣4ac>0;④a+b+c<0;⑤(a﹣2b+c)<0,其中正确的个数是( )

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD是一次函数y=x+1图象的其中一个伴侣正方形.
(1)若某函数是一次函数y=x+1,求它的图象的所有伴侣正方形的边长;

(2)若某函数是反比例函数![]() ,它的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式;
,它的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式;

(3)若某函数是二次函数y=ax2+c(a≠0),它的图象的伴侣正方形为ABCD,C、D中的一个点坐标为(3,4).写出伴侣正方形在抛物线上的另一个顶点坐标,写出符合题意的其中一条抛物线解析式,并判断你写出的抛物线的伴侣正方形的个数是奇数还是偶数?.(本小题只需直接写出答案)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一块长方形镜面玻璃的四周镶上与它的周长相等的边框,制成一面镜子,镜子的长与宽的比是2:1,已知镜面玻璃的价格是每平方米120元,边框的价格是每米30元,另外制作这面镜子还需加工费45元.设制作这面镜子的总费用是![]() 元,镜子的宽是
元,镜子的宽是![]() 米.
米.
(1)求![]() 与
与![]() 之间的关系式.
之间的关系式.
(2)如果制作这面镜子共花了195元,求这面镜子的长和宽.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,以点O为圆心的圆分别交x轴的正半轴于点M,交y轴的正半轴于点N.劣弧![]() 的长为
的长为![]() ,直线
,直线![]() 与x轴、y轴分别交于点A、B.
与x轴、y轴分别交于点A、B.
(1)求证:直线AB与⊙O相切;
(2)求图中所示的阴影部分的面积(结果用π表示)
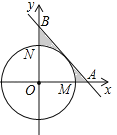
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com