
ЁОЬтФПЁПзлКЯгыЬНОП
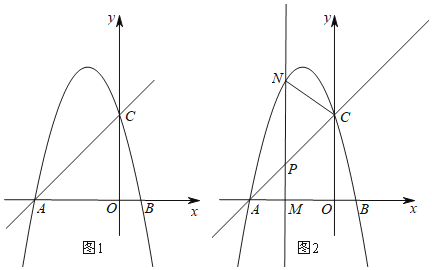
ШчЭМ1ЫљЪОЃЌжБЯпy=x+cгыxжсНЛгкЕуA(-4,0)ЃЌгыyжсНЛгкЕуCЃЌХзЮяЯпy=-x2+bx+cОЙ§ЕуAЃЌCЃЎ
(1)ЧѓХзЮяЯпЕФНтЮіЪН
(2)ЕуEдкХзЮяЯпЕФЖдГЦжсЩЯЃЌЧѓCE+OEЕФзюаЁжЕЃЛ
(3)ШчЭМ2ЫљЪОЃЌMЪЧЯпЖЮOAЕФЩЯвЛИіЖЏЕуЃЌЙ§ЕуMДЙжБгкxжсЕФжБЯпгыжБЯпACКЭХзЮяЯпЗжБ№НЛгкЕуPЁЂNЃЎ
ЂйШєвдCЃЌPЃЌNЮЊЖЅЕуЕФШ§НЧаЮгыЁїAPMЯрЫЦЃЌдђЁїCPNЕФУцЛ§ЮЊЁЁЁЁЃЛ
ЂкШєЕуPЧЁКУЪЧЯпЖЮMNЕФжаЕуЃЌЕуFЪЧжБЯпACЩЯвЛИіЖЏЕуЃЌдкзјБъЦНУцФкЪЧЗёДцдкЕуDЃЌЪЙвдЕуDЃЌFЃЌPЃЌMЮЊЖЅЕуЕФЫФБпаЮЪЧСтаЮЃПШєДцдкЃЌЧыжБНгаДГіЕуDЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
зЂЃКЖўДЮКЏЪ§y=ax2+bx+c(aЁй0)ЕФЖЅЕузјБъЮЊ(![]() )
)
ЁОД№АИЁП(1)y=-x2-3x+4ЃЛ(2)5ЃЛ(3)Ђй![]() Лђ4ЃЛЂкДцдкЃЌDЕузјБъЮЊ(
Лђ4ЃЛЂкДцдкЃЌDЕузјБъЮЊ(![]() ЃЌ
ЃЌ![]() )Лђ(-1+
)Лђ(-1+![]() ЃЌ
ЃЌ![]() )Лђ(-1-
)Лђ(-1-![]() ЃЌ-
ЃЌ-![]() )Лђ(-4ЃЌ3).
)Лђ(-4ЃЌ3).
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнвбжЊЬѕМўЧѓГіC,дйНЋЕуAДњШыМДПЩЧѓГіНтЮіЪН.
(2) зіЕу![]() ЙигкХзЮяЯпЕФЖдГЦжсжБЯп
ЙигкХзЮяЯпЕФЖдГЦжсжБЯп![]() ЕФЖдГЦЕу
ЕФЖдГЦЕу![]() ЃЌСЌ
ЃЌСЌ![]() ЃЌНЛжБЯп
ЃЌНЛжБЯп![]() гкЕу
гкЕу![]() ЃЎСЌ
ЃЎСЌ![]() ЃЌИљОнЙДЙЩЖЈРэМДПЩНтД№.
ЃЌИљОнЙДЙЩЖЈРэМДПЩНтД№.
(3)ЂйЗжРрЬжТлВЛЭЌЯрЫЦЧщПіЃЌРћгУЬѕМўЧѓГіЯпЖЮГЄЖШМДПЩНтД№.
ЂкЩш![]() зјБъЮЊ
зјБъЮЊ![]() ЃЌЕУГіPЕузјБъЃЌДњШыЪНзгЧѓГіaЃЌИљОнСтаЮаджЪМДПЩЧѓГіDЕузјБъ.
ЃЌЕУГіPЕузјБъЃЌДњШыЪНзгЧѓГіaЃЌИљОнСтаЮаджЪМДПЩЧѓГіDЕузјБъ.
(1)НЋ![]() ДњШы
ДњШы![]()
![]()
НЋ![]() КЭ
КЭ![]() ДњШы
ДњШы![]()
![]()
![]() ХзЮяЯпНтЮіЪНЮЊ
ХзЮяЯпНтЮіЪНЮЊ![]()
(2)зіЕу![]() ЙигкХзЮяЯпЕФЖдГЦжсжБЯп
ЙигкХзЮяЯпЕФЖдГЦжсжБЯп![]() ЕФЖдГЦЕу
ЕФЖдГЦЕу![]() ЃЌСЌ
ЃЌСЌ![]() ЃЌНЛжБЯп
ЃЌНЛжБЯп![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
СЌ![]() ЃЌДЫЪБ
ЃЌДЫЪБ![]() ЕФжЕзюаЁЃЎ
ЕФжЕзюаЁЃЎ
![]() ХзЮяЯпЖдГЦжсЮЛжУЯп
ХзЮяЯпЖдГЦжсЮЛжУЯп![]()
![]()
гЩЙДЙЩЖЈРэ![]()
![]() ЕФзюаЁжЕЮЊ5
ЕФзюаЁжЕЮЊ5
(3)ЂйЕБ![]() ЪБЃЌ
ЪБЃЌ
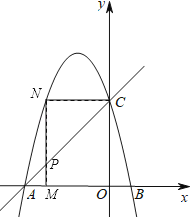
![]() ЃЌдђ
ЃЌдђ![]() ЙигкХзЮяЯпЖдГЦжсЖдГЦ
ЙигкХзЮяЯпЖдГЦжсЖдГЦ
![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]()
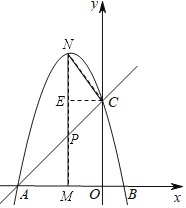
ЕБ![]() ЪБ
ЪБ
гЩвбжЊ![]() ЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ЮЊЕШбќжБНЧШ§НЧаЮЃЌ![]()
Й§Еу![]() зї
зї![]() гкЕу
гкЕу![]() ЃЌЩшЕу
ЃЌЩшЕу![]() зјБъЮЊ
зјБъЮЊ![]()
![]() ЃЌ
ЃЌ
дђ![]() ЮЊ
ЮЊ![]() ЃЌ
ЃЌ![]()
![]()
ДњШы![]()
НтЕУ![]()
![]() ЕФУцЛ§ЮЊ4
ЕФУцЛ§ЮЊ4
ЙЪД№АИЮЊЃК![]() Лђ4
Лђ4
ЂкДцдк
Щш![]() зјБъЮЊ
зјБъЮЊ![]()
дђ![]() ЮЊ
ЮЊ![]()
дђ![]() ЕузјБъЮЊ
ЕузјБъЮЊ![]()
АбЕу![]() зјБъДњШы
зјБъДњШы![]()
НтЕУ![]() (ЩсШЅ)ЃЌ
(ЩсШЅ)ЃЌ![]()
ЕБ![]() ЪБЃЌЕу
ЪБЃЌЕу![]() дк
дк![]() ДЙжБЦНЗжЯпЩЯЃЌдђ
ДЙжБЦНЗжЯпЩЯЃЌдђ![]()
ЕБ![]() ЪБЃЌгЩСтаЮаджЪЕу
ЪБЃЌгЩСтаЮаджЪЕу![]() зјБъЮЊ
зјБъЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЁЂ
ЁЂ![]() ЙигкжБЯп
ЙигкжБЯп![]() ЖдГЦЃЌЕу
ЖдГЦЃЌЕу![]() зјБъЮЊ
зјБъЮЊ![]()


 КЎМйДѓДЎСЊЛЦЩНЪщЩчЯЕСаД№АИ
КЎМйДѓДЎСЊЛЦЩНЪщЩчЯЕСаД№АИ КЎМйДДаТаЭзджїбЇЯАЕкШ§бЇЦкКЎМйЯЮНгЯЕСаД№АИ
КЎМйДДаТаЭзджїбЇЯАЕкШ§бЇЦкКЎМйЯЮНгЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
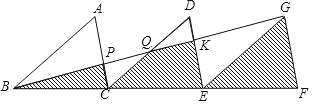
ЁОЬтФПЁПШчЭМЃЌвбжЊЁїABCЁеЁїDCEЁеЁїGEFЃЌШ§ЬѕЖдгІБпBCЃЎCEЁЂEFдкЭЌвЛЬѕжБЯпЩЯЃЌСЌНгBGЃЌЗжБ№НЛACЁЂDCЁЂDEгкЕуPЁЂQЁЂKЃЌЦфжаSЁїPQC=3ЃЌдђЭМжаШ§ИівѕгАВПЗжЕФУцЛ§КЭЮЊ__ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбЇаЃЮЊИФЩЦАьбЇЬѕМўЃЌМЦЛЎВЩЙКAЁЂBСНжжаЭКХЕФПеЕїЃЌвбжЊВЩЙК3ЬЈAаЭПеЕїКЭ2ЬЈBаЭПеЕїЃЌашЗбгУ39000дЊЃЛ4ЬЈAаЭПеЕїБШ5ЬЈBаЭПеЕїЕФЗбгУЖр6000дЊЃЎ
ЃЈ1ЃЉЧѓAаЭПеЕїКЭBаЭПеЕїУПЬЈИїашЖрЩйдЊЃЛ
ЃЈ2ЃЉШєбЇаЃМЦЛЎВЩЙКAЁЂBСНжжаЭКХПеЕїЙВ30ЬЈЃЌЧвAаЭПеЕїЕФЬЈЪ§ВЛЩйгкBаЭПеЕїЕФвЛАыЃЌСНжжаЭКХПеЕїЕФВЩЙКзмЗбгУВЛГЌЙ§217000дЊЃЌИУаЃЙВгаФФМИжжВЩЙКЗНАИЃП
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌВЩгУФФвЛжжВЩЙКЗНАИПЩЪЙзмЗбгУзюЕЭЃЌзюЕЭЗбгУЪЧЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЮЊЧьзЃЙњЧьНкОйАьгЮдАЛюЖЏЃЌаЁОќРДЕНУўЧђЖвНБЛюЖЏГЁЕиЃЌРюРЯЪІЖдаЁОќЫЕЃКЁАетРягаМзЁЂввСНИіКазгЃЌРяУцЖМзАгавЛаЉЦЙХвЧђЃЌФужЛФмбЁдёдкЦфжавЛИіКазгжаУўЧђЁЃЁБЛёНБЙцдђШчЯТЃК
МзКажагаАзЩЋЦЙХвЧђ4ИіЃЌЛЦЩЋЦЙХвЧђ1ИіЃЌвЛШЫжЛФмУўвЛДЮЧввЛДЮУўГівЛИіЧђЃЌШєетИіЧђЮЊЛЦЩЋЧђЃЌдђПЩЛёЕУЭцОпамвЛИіЃЌЗёдђВЛЕУНБЃЛ
ввКажагаАзЩЋЦЙХвЧђ2ИіЃЌЛЦЩЋЦЙХвЧђ3ИіЃЌвЛШЫжЛФмУўвЛДЮЧввЛДЮУўГіСНИіЧђЃЌШєетСНИіЧђОљЮЊЛЦЩЋЧђЃЌдђПЩЛёЕУЭцОпамвЛИіЃЌЗёдђВЛЕУНБЃЛ
ЧыЮЪаЁОќдкФФИіКазгФкУўЧђЛёЕУЭцОпамЕФЛњЛсИќДѓЃПЧыгУИХТЪжЊЪЖЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙигкxЕФвЛдЊЖўДЮЗНГЬx2+3x+m-1=0ЕФСНИіЪЕЪ§ИљЗжБ№ЮЊx1,x2ЃЎ
ЃЈ1ЃЉЧѓmЕФШЁжЕЗЖЮЇЃЎ
ЃЈ2ЃЉШє2ЃЈx1+x2ЃЉ+ x1x2+10=0ЃЎЧѓmЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЕЅЮЛЮЊ1ЕФЭјИёжаЃЌгаЁїABCЃЌЧвЕФШ§ИіЖЅЕуЖМдкИёЕуЩЯЃК
ЃЈ1ЃЉвдЕуCЮЊдЕуНЈСЂжБНЧзјБъЯЕЃЌВЂШЗЖЈAЕуЕФзјБъЃЛ
ЃЈ2ЃЉНЋЁїABCЯђЯТЦНвЦ5ИіЕЅЮЛЃЌЕУЕНЁїA1B1C1ЃЈВЛаДзїЗЈЃЉЃЛ
ЃЈ3ЃЉвдЕуCЮЊа§зЊжааФЃЌНЋЁїABCЫГЪБеыа§зЊ90ЁуЕУЕНЁїA2B2C2ЃЈВЛаДзїЗЈЃЉЃЛ
ЃЈ4ЃЉЧѓЛЁBB2ЕФГЄ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
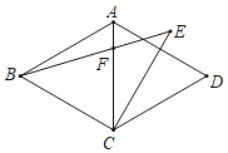
ЁОЬтФПЁПШчЭМЃЌдкСтаЮABCDжаЃЌЁЯBADЃН120ЁуЃЌCEЁЭADЃЌЧвCEЃНBCЃЌСЌНгBEНЛЖдНЧЯпACгкЕуFЃЌдђЁЯEFCЃН_____ЁуЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШє|m+3|+![]() ЃН0ЃЌЕуPЃЈmЃЌnЃЉЙигкxжсЕФЖдГЦЕуPЁфЮЊЖўДЮКЏЪ§ЭМЯѓЖЅЕуЃЌдђЖўДЮКЏЪ§ЕФНтЮіЪНЮЊЃЈЁЁЁЁЃЉ
ЃН0ЃЌЕуPЃЈmЃЌnЃЉЙигкxжсЕФЖдГЦЕуPЁфЮЊЖўДЮКЏЪ§ЭМЯѓЖЅЕуЃЌдђЖўДЮКЏЪ§ЕФНтЮіЪНЮЊЃЈЁЁЁЁЃЉ
A. yЃН![]() ЃЈxЉ3ЃЉ2+2B. yЃН
ЃЈxЉ3ЃЉ2+2B. yЃН![]() ЃЈx+3ЃЉ2Љ2
ЃЈx+3ЃЉ2Љ2
C. yЃН![]() ЃЈxЉ3ЃЉ2Љ2D. yЃН
ЃЈxЉ3ЃЉ2Љ2D. yЃН![]() ЃЈx+3ЃЉ2+2
ЃЈx+3ЃЉ2+2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЪЧвЛзљЙХЙАЧХЕФНиУцЭМЃЌЙАЧХЧХЖДЕФЩЯбиЪЧХзЮяЯпаЮзДЃЌЕБЫЎУцЕФПэЖШЮЊ10mЪБЃЌЧХЖДгыЫЎУц
ЕФзюДѓОрРыЪЧ5mЃЎ
ЃЈ1ЃЉОЙ§ЬжТлЃЌЭЌбЇУЧЕУГіШ§жжНЈСЂЦНУцжБНЧзјБъЯЕЕФЗНАИЃЈШчЯТЭМЃЉ
ФубЁдёЕФЗНАИЪЧ_____ЃЈЬюЗНАИвЛЃЌЗНАИЖўЃЌЛђЗНАИШ§ЃЉЃЌдђBЕузјБъЪЧ______ЃЌЧѓГіФуЫљбЁЗНАИжаЕФХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉвђЮЊЩЯгЮЫЎПтаЙКщЃЌЫЎУцПэЖШБфЮЊ6mЃЌЧѓЫЎУцЩЯеЧЕФИпЖШЃЎ


ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com