Question

【题目】如图，平面直角坐标系中，直线AB交y轴于点A（0，1），交x轴于点B（3，0）．直线x=1交AB于点D，交x轴于点E，P是直线x=1上一动点，在点D的上方，设P（1，n）．

（1）求直线AB的解析式；

（2）求△ABP的面积（用含n的代数式表示）；

（3）当S△ABP=2时，以PB为边在第一象限作等腰直角三角形BPC，求出点C的坐标．

Answer 1

【答案】（1）y=x+1；（2）；（3）点C的坐标是（3，4）或（5，2）或（3，2）．

【解析】

（1）把的坐标代入直线的解析式，即可求得的值，然后在解析式中，令，求得的值，即可求得的坐标；

（2）利用即可求出结果；

（3）分三种情况讨论，当、、分别为等腰直角三角形的直角顶点时，求出点的坐标分别为、、。

(1)设直线AB的解析式是y=kx+b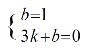

把A（0，1），B（3，0）代入得：

解得：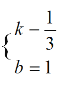

∴直线AB的解析式是:

（2）过点A作AM⊥PD，垂足为M，则有AM=1，

∵x=1时，=，P在点D的上方，

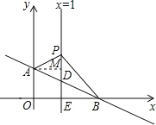
∴PD=n﹣，

由点B（3，0），可知点B到直线x=1的距离为2，即△BD的边PD上的高长为2，

∴，

∴；

（3）当S△ABP=2时，，解得n=2，∴点P（1，2）．

∵E（1，0）， ∴PE=BE=2，

∴∠EPB=∠EBP=45°．

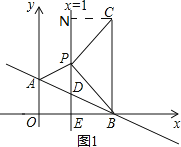
第1种情况，如图1，∠CPB=90°，BP=PC，

过点C作CN⊥直线x=1于点N．

∵∠CPB=90°，∠EPB=45°，

∴∠NPC=∠EPB=45°．

又∵∠CNP=∠PEB=90°，BP=PC，

∴△CNP≌△BEP，∴PN=NC=EB=PE=2，

∴NE=NP+PE=2+2=4， ∴C（3，4）．

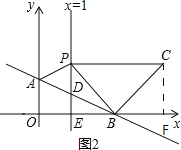
第2种情况，如图2, ∠PBC=90°，BP=BC，

过点C作CF⊥x轴于点F．

∵∠PBC=90°，∠EBP=45°，

∴∠CBF=∠PBE=45°．

又∵∠CFB=∠PEB=90°，BC=BP，

∴△CBF≌△PBE．

∴BF=CF=PE=EB=2，

∴OF=OB+BF=3+2=5， ∴C（5，2）．

3种情况，如图3，∠PCB=90°，

∴∠CPB=∠EBP=45°，

∴△PCB≌△ BEP，

∴PC=CB=PE=EB=2，∴C（3，2）．

∴以PB为边在第一象限作等腰直角三角形BPC，

综上所述点C的坐标是（3，4）或（5，2）或（3，2）．