
【题目】2018年9月28日,重庆八中80周年校庆在渝北校区隆重举行,学校总务处购买了红,黄,蓝三种花卉装扮出甲,乙,丙,丁四种造型,其中一个甲造型需要15盆红花,10盆黄花,10盆蓝花;一个乙造型需要5盆红花,7盆黄花,6盆蓝花;一个丙造型需要7盆红花,8盆黄花,9盆蓝花;一个丁造型需要6盆红花,4盆黄花,4盆蓝花,若一个甲造型售价1800元,利润率为20%,一个乙和一个丙造型一共成本和为1830元,且一盆红花的利润率为25%,问一个丁造型的利润率为_____.
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
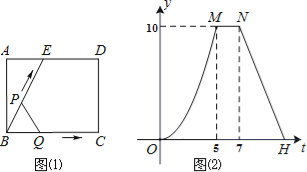
【题目】如图(1)所示,E为矩形ABCD的边AD上一点,动点P,Q同时从点B出发,点P沿折线BE-ED-DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(曲线OM为抛物线的一部分),则下列结论:①AD=BE=5;②![]() ;③当0<t≤5时,
;③当0<t≤5时,![]() ;④当
;④当![]() 秒时,△ABE∽△QBP;其中正确的结论是( )
秒时,△ABE∽△QBP;其中正确的结论是( )
A. ①②③B. ②③C. ①③④D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线型拱桥,当拱顶离水面![]() 时,水面宽
时,水面宽![]() 为
为![]() .当水面上升
.当水面上升![]() 时达到警戒水位,此时拱桥内的水面宽度是多少
时达到警戒水位,此时拱桥内的水面宽度是多少![]() ?
?
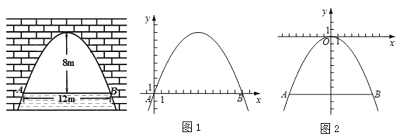
下面给出了解决这个问题的两种方法,请补充完整:
方法一:如图1.以点![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系
轴,建立平面直角坐标系![]() ,此时点
,此时点![]() 的坐标为_______,抛物线的项点坐标为_______,可求这条抛物线所表示的二次函数解析式为_______.当
的坐标为_______,抛物线的项点坐标为_______,可求这条抛物线所表示的二次函数解析式为_______.当![]() 时,求出此时自变量
时,求出此时自变量![]() 的取值,即可解决这个问题.
的取值,即可解决这个问题.
方法二:如图2,以抛物线顶点为原点,对称轴为![]() 轴.建立平面直角坐标系
轴.建立平面直角坐标系![]() ,这时这条抛物线所表示的二次函数的解析式为_______,当水面达到警戒水位,即
,这时这条抛物线所表示的二次函数的解析式为_______,当水面达到警戒水位,即![]() _______时,求出此时自变量
_______时,求出此时自变量![]() 的取值为_______,从而得水面宽为
的取值为_______,从而得水面宽为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 、 点
、 点![]() 分别在线段
分别在线段![]() 和线段
和线段![]() 上,
上, ![]() 平分
平分![]() .
.
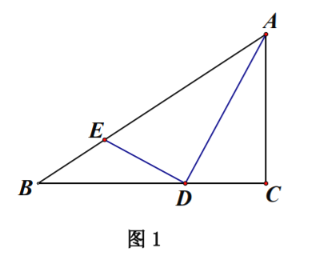
![]() 如图1,求证:
如图1,求证:![]() .
.
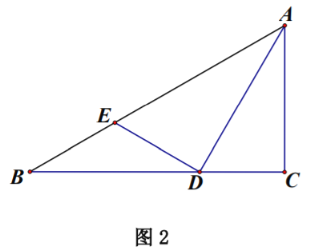
![]() 如图2,若
如图2,若![]() .求证:
.求证:![]() .
.
![]() 在
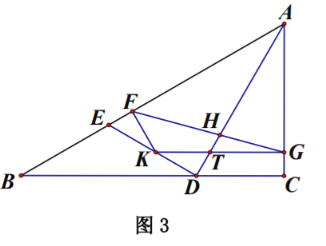
在![]() 问的条件下,如图3, 在线段
问的条件下,如图3, 在线段![]() 上取一点
上取一点![]() ,使
,使![]() .过点
.过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成(1),(2)两题
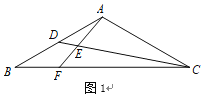
数学课上,老师出示了这样一道题:如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 上一点,且满足
上一点,且满足![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,求
,求![]() 的值.同学们经过思考后,交流了自己的想法:
的值.同学们经过思考后,交流了自己的想法:
小明:“通过观察和度量,发现![]() 与
与![]() 相等.”
相等.”
小伟:“通过构造全等三角形,经过进一步推理,就可以求出![]() 的值.”
的值.”
……
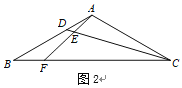
老师:“把原题条件中的‘![]() ’,改为‘
’,改为‘![]() ’其他条件不变(如图2),也可以求出
’其他条件不变(如图2),也可以求出![]() 的值.
的值.
(1)在图1中,①求证:![]() ;②求出
;②求出![]() 的值;
的值;
(2)如图2,若![]() ,直接写出
,直接写出![]() 的值(用含
的值(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
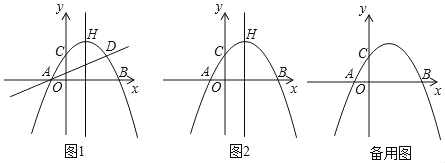
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0)和点B,与y轴交于点C,点C关于抛物线对称轴的对称点为点D,抛物线顶点为H(1,2).
(1)求抛物线的解析式;
(2)点P为直线AD上方抛物线的对称轴上一动点,连接PA,PD.当S△PAD=3,若在x轴上存在一动点Q,使PQ+![]() QB最小,求此时点Q的坐标及PQ+
QB最小,求此时点Q的坐标及PQ+![]() QB的最小值;
QB的最小值;
(3)若点E为抛物线上的动点,点G,F为平面内的点,以BE为边构造以B,E,F,G为顶点的正方形,当顶点F或者G恰好落在y轴上时,求点E的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
如果函数 y=f(x)满足:对于自变量 x 的取值范围内的任意 x1,x2,
(1)若 x1<x2,都有 f(x1)<f(x2),则称 f(x)是增函数;
(2)若 x1<x2,都有 f(x1)>f(x2),则称 f(x)是减函数.
例题:证明函数f(x)=![]() (x>0)是减函数.
(x>0)是减函数.
证明:设 0<x1<x2,
f(x1)﹣f(x2)=![]() .
.
∵0<x1<x2,
∴x2﹣x1>0,x1x2>0.
∴![]() >0.即 f(x1)﹣f(x2)>0.
>0.即 f(x1)﹣f(x2)>0.
∴f(x1)>f(x2).
∴函数 f(x)=![]() (x>0)是减函数.
(x>0)是减函数.
根据以上材料,解答下面的问题:
已知函数![]() .
.
f(﹣1)=![]() +(﹣2)=-1,f(﹣2)=
+(﹣2)=-1,f(﹣2)=![]() +(﹣4)=
+(﹣4)=![]() .
.
(1)计算:f(﹣3)= ,f(﹣4)= ;
(2)猜想:函数![]() 是 函数(填“增”或“减”);
是 函数(填“增”或“减”);
(3)请仿照例题证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与直线
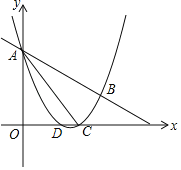
与直线![]() 交于A,B两点,交x轴与D,C两点,连接AC,已知A(0,3),C(3,0).(1)抛物线的解析式__;(2)设E为线段AC上一点(不含端点),连接DE,一动点M从点D出发,沿线段DE以每秒一个单位速度运动到E点,再沿线段EA以每秒
交于A,B两点,交x轴与D,C两点,连接AC,已知A(0,3),C(3,0).(1)抛物线的解析式__;(2)设E为线段AC上一点(不含端点),连接DE,一动点M从点D出发,沿线段DE以每秒一个单位速度运动到E点,再沿线段EA以每秒![]() 个单位的速度运动到A后停止.若使点M在整个运动中用时最少,则点E的坐标__.
个单位的速度运动到A后停止.若使点M在整个运动中用时最少,则点E的坐标__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等边△ABC的边长为8,点P是AB边上的一个动点(与点A、B不重合),直线l是经过点P的一条直线,把△ABC沿直线l折叠,点B的对应点是点B’.
(1)如图1,当PB=4时,若点B’恰好在AC边上,则AB’的长度为_____;
(2)如图2,当PB=5时,若直线l//AC,则BB’的长度为 ;
(3)如图3,点P在AB边上运动过程中,若直线l始终垂直于AC,△ACB’的面积是否变化?若变化,说明理由;若不变化,求出面积;
(4)当PB=6时,在直线l变化过程中,求△ACB’面积的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com