
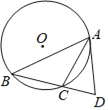
【题目】如图,⊙O是△ABC的外接圆,过点A作⊙O的切线交BC的延长线于点D.
(1)求证:∠CAD=∠B.
(2)若AC是∠BAD的平分线,sinB=![]() ,BC=2.求⊙O的半径.
,BC=2.求⊙O的半径.
【答案】(1)见解析;(2)⊙O的半径为![]() .
.
【解析】
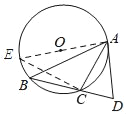
(1)连结AO,并延长AO交⊙O与点E,连结EC,依据圆周角定理可得到∠B=∠E,然后根据直径所对的圆周角为90°,得出∠E+∠EAC=90°,再根据切线的性质可得∠EAC+∠CAD=90°,进行证明即可;
(2)根据AC是∠BAD的平分线,结合(1)中结论证出BC=AC,然后由∠B=∠E可得到sinE=![]() ,从而可求得AE的长,然后可求得⊙O的半径.
,从而可求得AE的长,然后可求得⊙O的半径.
解:(1)连结AO,并延长AO交⊙O与点E,连结EC.
∵AD为⊙O的切线,
∴OA⊥AD,
∴∠EAD=90°,
∴∠EAC+∠CAD=90°.
∵AE为⊙O的直径,
∴∠E+∠EAC=90°,
∴∠E=∠CAD.
又∵∠E=∠B,
∴∠CAD=∠B.
(2)∵AC是∠BAD的平分线,
∴∠BAC=∠CAD.
又∵∠CAD=∠B,
∴∠BAC=∠CAB.
∴AC=BC=2.
又∵∠E=∠B,
∴∠CAD=∠B.
∴sinE=sinB=![]() ,
,
在Rt![]() AEC中,sinE=
AEC中,sinE=![]() ,
,
即![]() =
=![]() ,解得AE=
,解得AE=![]() ,
,
∴⊙O的半径为![]() .
.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
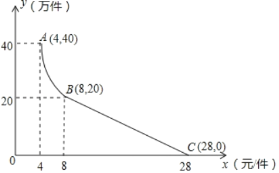
【题目】某科技有限公司用160万元作为新产品的研发费用,成功研制出了一种市场急需的电子产品,已于当年投入生产并进行销售.已知生产这种电子产品的成本为4元/件,在销售过程中发现:每年的年销售量y(万件)与销售价格x(元/件)的关系如图所示,其中AB为反比例函数图象的一部分,设公司销售这种电子产品的年利润为s(万元).(注:若上一年盈利,则盈利不计入下一年的年利润,若上一年亏损,则亏损记作下一年的成本)
(1)请求出y(万件)与x(元/件)的函数表达式;
(2)求出第一年这种电子产品的年利润s(万元)与x(元/件)的函数表达式,并求出第一年年利润的最大值;
(3)假设公司的这种电子产品第一年恰好按年利润s(万元)取得最大值时进行销售,现根据第一年的盈亏情况,决定第二年这种电子产品每件的销售价格x(元/件)定在8元以上(x>8),当第二年的年利润不低于103万元时,请结合年利润s(万元)与销售价格x(元/件)的函数示意图,求销售价格x(元/件)的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一粒木质中国象棋子“兵”,它的正面雕刻一个“兵”字,它的反面是平的![]() 将它从一定高度下掷,落地反弹后可能是“兵”字面朝上,也可能是“兵”字面朝下
将它从一定高度下掷,落地反弹后可能是“兵”字面朝上,也可能是“兵”字面朝下![]() 由于棋子的两面不均匀,为了估计“兵”字面朝上的概率,某实验小组做了棋子下掷实验,实验数据如下表:
由于棋子的两面不均匀,为了估计“兵”字面朝上的概率,某实验小组做了棋子下掷实验,实验数据如下表:
实验次数n | 20 | 60 | 100 | 120 | 140 | 160 | 500 | 1000 | 2000 | 5000 |
“兵”字面朝上次数m | 14 | 38 | 52 | 66 | 78 | 88 | 280 | 550 | 1100 | 2750 |
“兵”字面朝上频率 |
|
|
|
|
|
|
|
|
|
|
下面有三个推断:![]() 投掷1000次时,“兵”字面朝上的次数是550,所以“兵”字面朝上的概率是
投掷1000次时,“兵”字面朝上的次数是550,所以“兵”字面朝上的概率是![]() ;
;![]() 随着实验次数的增加,“兵”字面朝上的频率总在
随着实验次数的增加,“兵”字面朝上的频率总在![]() 附近,显示出一定的稳定性,可以估计“兵”字面朝上的概率是
附近,显示出一定的稳定性,可以估计“兵”字面朝上的概率是![]() ;
;![]() 当实验次数为200次时,“兵”字面朝上的频率一定是
当实验次数为200次时,“兵”字面朝上的频率一定是![]() 其中合理的是
其中合理的是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某日的钱塘江观潮信息如表:

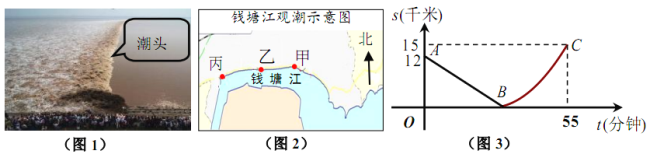
按上述信息,小红将“交叉潮”形成后潮头与乙地之间的距离![]() (千米)与时间
(千米)与时间![]() (分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点
(分钟)的函数关系用图3表示,其中:“11:40时甲地‘交叉潮’的潮头离乙地12千米”记为点![]() ,点
,点![]() 坐标为
坐标为![]() ,曲线
,曲线![]() 可用二次函数
可用二次函数![]() (
(![]() ,
,![]() 是常数)刻画.
是常数)刻画.
(1)求![]() 的值,并求出潮头从甲地到乙地的速度;
的值,并求出潮头从甲地到乙地的速度;
(2)11:59时,小红骑单车从乙地出发,沿江边公路以![]() 千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
千米/分的速度往甲地方向去看潮,问她几分钟后与潮头相遇?
(3)相遇后,小红立即调转车头,沿江边公路按潮头速度与潮头并行,但潮头过乙地后均匀加速,而单车最高速度为![]() 千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度
千米/分,小红逐渐落后,问小红与潮头相遇到落后潮头1.8千米共需多长时间?(潮水加速阶段速度![]() ,
,![]() 是加速前的速度).
是加速前的速度).
查看答案和解析>>
科目:初中数学 来源: 题型:
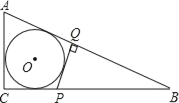
【题目】如图,⊙O内切于Rt△ABC,点P、点Q分别在直角边BC、斜边AB上,PQ⊥AB,且PQ与⊙O相切,若AC=2PQ,则tan∠B的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交
于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=mx2+(5m+3)x+4m(m为常数且m≠0)有以下三种说法:
①不论m为何值,函数图象一定过定点(﹣1,﹣3);
②当m=﹣1时,函数图象与坐标轴有3个交点;
③当m<0,x≥﹣![]() 时,函数y随x的增大而减小;判断真假,并说明理由.
时,函数y随x的增大而减小;判断真假,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
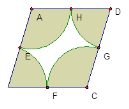
【题目】如图,菱形ABCD,边长等于2,点E、F、G、H分别是AB、BC、CD、DA的中点,图中阴影部分由四个小扇形组成,对于下列判断中正确的有( )
①空白图形空白部分的周长=2![]() ②空白部分的面积=
②空白部分的面积=![]()
③四个小扇形的面积和 =![]() ④菱形的面积=4
④菱形的面积=4
A 1个 B 2个 C 3个 D 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6, ![]() .求BE的长.
.求BE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com