Question

如图，抛物线y=x²﹣2x﹣3与x轴交A、B两点（A点在B点左侧），直线l与抛物线交于A、C两点，其中C点的横坐标为2．                                                                                                    

（1）求A、B两点的坐标及直线AC的函数表达式；                                      

（2）P是线段AC上的一个动点，过P点作y轴的平行线交抛物线于E点，求线段PE长度的最大值．                  

                                                        

　                                                                                                      

                                                                                                          

Answer 1

【考点】二次函数综合题．                                                                     

【专题】压轴题；动点型．                                                                     

【分析】（1）令y=0，解x²﹣2x﹣3=0，可得AB的坐标；将C的横坐标代入，易得其纵坐标，结合A的坐标，可ACC的方程；                                                                                               

（2）设出P点的横坐标，表示出P、E的坐标，可得PE长度的表达式，进而根据x的取值范围可得线段PE长度的最大值．                                                                       

【解答】解：（1）令y=0，解得x₁=﹣1或x₂=3，                                          

∴A（﹣1，0）B（3，0）；                                                                    

将C点的横坐标x=2代入y=x²﹣2x﹣3                                                     

得y=﹣3，                                                                                         

∴C（2，﹣3），                                                                               

设直线AC的解析式是y=kx+b，                                                              

把A（﹣1，0），C（2，﹣3）代入得：，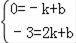                                  

解得：k=﹣1，b=﹣1，                                                                            

∴直线AC的函数解析式是y=﹣x﹣1；                                                    

                                                                                                          

（2）设P点的横坐标为x（﹣1≤x≤2）（注：x的范围不写不扣分）               

则P、E的坐标分别为：P（x，﹣x﹣1），E（x，x²﹣2x﹣3）                       

∵P点在E点的上方，PE=（﹣x﹣1）﹣（x²﹣2x﹣3）=﹣x²+x+2=﹣（x﹣）²+，                 

∴当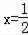时，PE的最大值=．