
已知,如图CD是⊙O的切线,C是切点,直径AB的延长线与CD相交于D,连接OC、BC.
(1)写出三个不同类型的结论;
(2)若BD=OB,求证:CA=CD.


【考点】切线的性质.
【专题】开放型.
【分析】(1)CD是圆的切线可得出的有:OC⊥CD(切线的性质),CD2=DBDA(切线长定理),△BCD∽△CAD(弦切角定理),AB是圆的直角可得出的有∠ACB=90°(圆周角定理)等.只要正确的都可以;
(2)由BD=OB可知,BC是直角三角形OCD底边上的中线,因此BC=OB=OD.因此三角形OBC就是个等边三角形,因此∠COB=60°,也就求出了∠D=30°,然后根据等边对等角,且外角为60°可在三角形OAC中求出∠A=30°,然后根据等角对等边即可得出CA=CD.
【解答】(1)解:不同类型的结论有:
△BCD∽△CAD,
OC⊥CD,
△ABC是直角三角形,
OC2+CD2=OD2,
CD2=DBDA,
∠ECD=∠OCA;
(2)证明:∵CD是圆O的切线,
∴OC⊥CD,
∵OB=BD,
∴BC是直角三角形OCD斜边上的中线,
∴BD=OB=BC=OC,
∴△OBC是等边三角形,
∴∠COB=60°,
∴∠D=90﹣60=30°;
∵OA=OC,
∴∠A=∠OCA=30°,
∴∠A=∠D,
即CA=AD.
【点评】本题主要考查了切线的性质,圆周角定理,等边三角形的性质等知识点的综合运用.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
一座建筑物发生了火灾,消防车到达现场后,发现最多只能靠近建筑物底端5米,消防车的云梯最大升长为13米,则云梯可以达该建筑物的最大高度是( )
A.12米 B.13米 C.14米 D.15米
查看答案和解析>>
科目:初中数学 来源: 题型:
点P在∠AOB的平分线上,点P到OA边的距离等于3,点Q是OB边上任意一点,下列关于线段PQ长度的描述正确的是( )
A.PQ>3 B.PQ≥3 C.PQ<3 D.PQ≤3
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,抛物线y=x2﹣2x﹣3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求A、B两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值.


查看答案和解析>>
科目:初中数学 来源: 题型:
某农场租用播种机播种小麦,在甲播种机播种2天后,又调来乙播种机参与播种,直至完成800亩的播种任务,播种亩数与天数之间的函数关系如图所示,那么乙播种机参与播种的天数是 天.
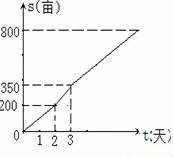

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com