
在Rt△ABC中,∠A=90°,有一个锐角为60°,BC=6.若点P在直线AC上(不与点A,C重合),且∠ABP=30°,则CP的长为 .
6或2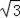
 或4
或4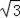
 .
.
【考点】解直角三角形.
【专题】压轴题;分类讨论.
【分析】根据题意画出图形,分4种情况进行讨论,利用直角三角形的性质解答.
【解答】解:如图1:
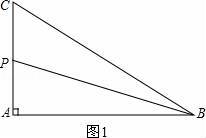

当∠C=60°时,∠ABC=30°,与∠ABP=30°矛盾;
如图2:


当∠C=60°时,∠ABC=30°,
∵∠ABP=30°,
∴∠CBP=60°,
∴△PBC是等边三角形,
∴CP=BC=6;
如图3:
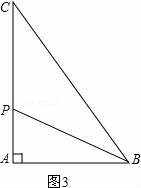

当∠ABC=60°时,∠C=30°,
∵∠ABP=30°,
∴∠PBC=60°﹣30°=30°,
∴PC=PB,
∵BC=6,
∴AB=3,
∴PC=PB=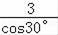
 =
=
 =2
=2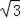
 ;
;
如图4:
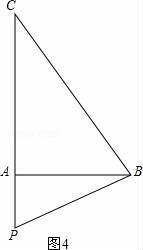

当∠ABC=60°时,∠C=30°,
∵∠ABP=30°,
∴∠PBC=60°+30°=90°,
∴PC=BC÷cos30°=4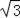
 .
.
故答案为:6或2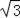
 或4
或4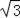
 .
.
【点评】本题考查了解直角三角形,熟悉特殊角的三角函数值是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
已知∠MON,用三角尺按下列方法画图:
在∠MON的两边OM,ON上,分别取OA=OB,再分别过点A,B作ON,OM的垂线AD,BE,交ON,OM于点D,E,两条垂线相交于点C,作射线OC,则射线OC平分∠MON.
问:
(1)△AOD与△BOE全等吗?(不需证明)
(2)请利用(1)的结论证明射线OC平分∠MON.

查看答案和解析>>
科目:初中数学 来源: 题型:
已知,如图CD是⊙O的切线,C是切点,直径AB的延长线与CD相交于D,连接OC、BC.
(1)写出三个不同类型的结论;
(2)若BD=OB,求证:CA=CD.


查看答案和解析>>
科目:初中数学 来源: 题型:
已知:点A(x1,y1)、B(x2,y2)、C(x3,y3)是函数y=﹣
 图象上的三点,且x1<0<x2<x3则y1、y2、y3的大小关系是( )
图象上的三点,且x1<0<x2<x3则y1、y2、y3的大小关系是( )
A.y1<y2<y3 B.y2<y3<y1 C.y3<y2<y1 D.无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com