
【题目】在平面直角坐标系中,我们把经过同一点的所有直线称为过这一点的直线束,如下图,所有经过点P的直线,称为过点P的直线束.

例如:直线y=kx,当k取不同实数时,在图象上可以得到过原点(0,0)的直线束,这个直线束的一般表达式为y=kx.
(1)当k取不同实数时,y=kx﹣3是过点( , )的直线束;
(2)当k取什么实数时,直线束y=kx﹣3中的直线与x轴、y轴围成的三角形面积为3?
(3)当k取什么实数时,直线束y=kx﹣2k+3中的直线与x轴、y轴围成的三角形面积为12?
【答案】(1)(0,﹣3);(2)当k取![]() 或﹣
或﹣![]() 时,直线束y=kx﹣3中的直线与x轴、y轴围成的三角形面积为3;(3)当k=
时,直线束y=kx﹣3中的直线与x轴、y轴围成的三角形面积为3;(3)当k=![]() 或k=﹣
或k=﹣![]() 时,直线束y=kx﹣2k+3中的直线与x轴、y轴围成的三角形面积为12.
时,直线束y=kx﹣2k+3中的直线与x轴、y轴围成的三角形面积为12.
【解析】
(1)当x=0时,y=-3,可以确定y=kx-3是过点(0,-3)的直线束;
(2)中分别求出直线束与x轴、y轴的交点坐标,再由直线与坐标轴围成的三角形是直角三角形,根据直角三角形的面积求法,列出相应的等式,进而求出满足条件的值;
(3)和(2)方法相同.
解:(1)∵y=kx﹣3,当x=0时,y=﹣3,
∴直线y=kx﹣3恒经过点(0,﹣3),
∴当k取不同实数时,y=kx﹣3是过点( 0,﹣3)的直线束,
故答案为(0,﹣3);
(2)在y=kx﹣3中,令y=0,则x=![]() ;令x=0,则y=﹣3,
;令x=0,则y=﹣3,
∴直线束y=kx﹣3中的直线与x轴、y轴的交点为(![]() ,0),(0,﹣3),
,0),(0,﹣3),
∵围成的三角形面积为3,
∴![]() |
|![]() |×3=3,
|×3=3,
解得:k=±![]() ,
,
∴当k取![]() 或﹣时
或﹣时![]() ,直线束y=kx﹣3中的直线与x轴、y轴围成的三角形面积为3;
,直线束y=kx﹣3中的直线与x轴、y轴围成的三角形面积为3;
(3)在直线束y=kx﹣2k+3中,令y=0,则x=![]() ;令x=0,则y=﹣2k+3,
;令x=0,则y=﹣2k+3,
∴直线束y=kx﹣2k+3中的直线与x轴、y轴的交点为(![]() ,0),(0,﹣2k+3),
,0),(0,﹣2k+3),
∵围成的三角形面积为12,
∴![]() |
|![]() |·|﹣2k+3|
|·|﹣2k+3|
当k>0时,4k2﹣36k+9=0,
∴k=![]() ,
,
当k<0时,4k2+12k+9=0,
∴k=﹣![]() ;
;
综上所述:当k=![]() 或k=﹣
或k=﹣![]() 时,直线束y=kx﹣2k+3中的直线与x轴、y轴围成的三角形面积为12.
时,直线束y=kx﹣2k+3中的直线与x轴、y轴围成的三角形面积为12.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】某班级组织了“我和我的祖国”演讲比赛,甲、乙两队各有10人参加本次比赛,成绩如下(10分制)
甲 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
乙 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
(1)甲队成绩的众数是 分,乙队成绩的中位数是 分.
(2)计算乙队成绩的平均数和方差.
(3)已知甲队成绩的方差是1分2,则成绩较为整齐的是 队.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,且点E在线段AD上,若AF=4,∠F=60°.
(1)指出旋转中心和旋转角度;
(2)求DE的长度和∠EBD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖、小明、小亮在解方程![]() 时,解法各不相同,请你回答下列问题:
时,解法各不相同,请你回答下列问题:
(1)简要分析一下三位同学的解法是否正确.如果正确,他运用了哪种解一元二次方程的方法;如果错误,错误的原因是什么?你是否从中体会到解一元二次方程的数学思想是什么?
(2)请你选择一种你熟练的方法尝试解一元二次方程![]() .
.
由方程 因此 所以这个数是0或3 | 方程
|
即 或 所以这个数是0或3. |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年某市为创评“全国文明城市”称号,周末团市委组织志愿者进行宣传活动.班主任梁老师决定从4名女班干部(小悦、小惠、小艳和小倩)中通过抽签的方式确定2名女生去参加.
抽签规则:将4名女班干部姓名分别写在4张完全相同的卡片正面,把四张卡片背面朝上,洗匀后放在桌面上,梁老师先从中随机抽取一张卡片,记下姓名,再从剩余的3张卡片中随机抽取第二张,记下姓名.
(1)该班男生“小刚被抽中”是 事件,“小悦被抽中”是 事件(填“不可能”或“必然”或“随机”);第一次抽取卡片“小悦被抽中”的概率为 ;
(2)试用画树状图或列表的方法表示这次抽签所有可能的结果,并求出“小惠被抽中”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=5,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE.延长AF交边BC于点G,则CG为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
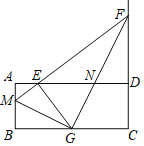
【题目】在矩形ABCD中,AB=4,AD=10,E是AD的一点,且AE=2,M是AB上一点,射线ME交CD的延长线于点F,EG⊥ME交BC于点G,连接MG,FG,FG交AD于点N.
(1)当点M为AB中点时,则DF= ,FG= .(直接写出答案)
(2)在整个运动过程中,![]() 的值是否会变化,若不变,求出它的值;若变化,请说明理由.
的值是否会变化,若不变,求出它的值;若变化,请说明理由.
(3)若△EGN为等腰三角形时,请求出所有满足条件的AM的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E,连结OE,CD=![]() ,∠ACB=30°.
,∠ACB=30°.
(1)求证:DE是⊙O的切线;
(2)分别求AB,OE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车都从A地驶向B地,并以各自的速度匀速行驶![]() 甲车比乙车早行驶,甲车途中休息了
甲车比乙车早行驶,甲车途中休息了![]() 设甲车行驶时间为
设甲车行驶时间为![]() ,下图是甲乙两车行驶的距离
,下图是甲乙两车行驶的距离![]() 与
与![]() 的函数图象,根据题中信息回答问题:
的函数图象,根据题中信息回答问题:
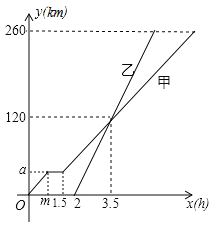
![]() 填空:
填空:![]() ______,
______,![]() ______;
______;
![]() 当乙车出发后,求乙车行驶路程
当乙车出发后,求乙车行驶路程![]() 与
与![]() 的函数解析式,并写出相应的x的取值范围;
的函数解析式,并写出相应的x的取值范围;
![]() 当甲车行驶多长时间时,两车恰好相距50km?请直接写出答案.
当甲车行驶多长时间时,两车恰好相距50km?请直接写出答案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com