
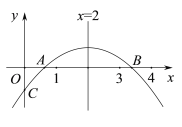
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论:①abc>0;②9a+3b+c<0;③c>﹣1;④关于x的方程ax2+bx+c=0(a≠0)有一个根为![]() ,其中正确结论的个数为( )
,其中正确结论的个数为( )
A. 1B. 2C. 3D. 4
【答案】C
【解析】
由二次函数图象的开口方向、对称轴及与y轴的交点可分别判断出a、b、c的符号,从而可判断①;由图象可知当x=3时,y>0,可判断②;由OA=OC,且OA<
1,可判断③;把![]() 代入方程整理可得ac2-bc+c=0,结合③可判断④;从而可得出答案.
代入方程整理可得ac2-bc+c=0,结合③可判断④;从而可得出答案.
解:由图象开口向下,可知a<0,
与y轴的交点在x轴的下方,可知c<0,
又对称轴方程为x=2,所以![]() ,所以b>0,
,所以b>0,
∴abc>0,故①正确;
由图象可知当x=3时,y>0,
∴9a+3b+c>0,故②错误;
由图象可知OA<1,
∵OA=OC,
∴OC<1,即-c<1,c>-1,故③正确:
假设方程的一个根为x=![]() ,把x=
,把x=![]() 代入方程可得
代入方程可得![]() ,
,
整理可得ac-b+1=0,
两边同时乘c可得ac2-bc+c=0,即方程有一个根为x=-c,
由②可知-c=OA,而x=OA是方程的根,
∴x=-c是方程的根,即假设成立,故④正确;综上可知正确的结论有三个;
故答案为C.


科目:初中数学 来源: 题型:
【题目】图中是小明完成的一道作业题,请你参考小明的解答方法解答下面的问题:
小明的作业
计算:(-4)7×0.257
解:(-4)7×0.257=(-4×0.25)7
=(-1)7
=-1
(1)计算①82018×(-0.125)2018② ![]()
(2)看2·4n·16n=219 , 求n的值
查看答案和解析>>
科目:初中数学 来源: 题型:
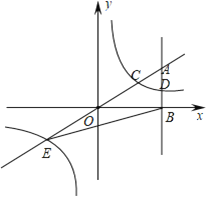
【题目】如图,在平面直角坐标系中,A点的坐标为(a,6),AB⊥x轴于点B,![]() =
=![]() ,反比例函数y=
,反比例函数y=![]() 的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为
的图象的一支分别交AO、AB于点C、D.延长AO交反比例函数的图象的另一支于点E.已知点D的纵坐标为![]() .
.
(1)求反比例函数的解析式及点E的坐标;
(2)连接BC,求S△CEB.
(3)若在x轴上的有两点M(m,0)N(-m,0).
①以E、M、C、N为顶点的四边形能否为矩形?如果能求出m的值,如果不能说明理由.
②若将直线OA绕O点旋转,仍与y=![]() 交于C、E,能否构成以E、M、C、N为顶点的四边形为菱形,如果能求出m的值,如果不能说明理由.
交于C、E,能否构成以E、M、C、N为顶点的四边形为菱形,如果能求出m的值,如果不能说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
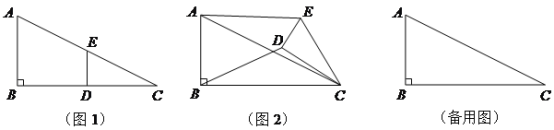
【题目】(10分)如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE. 将△EDC绕点C按顺时针方向旋转,记旋转角为α.
(1)问题发现
① 当![]() 时,
时,![]() ;② 当
;② 当![]() 时,
时,![]()
(2)拓展探究
试判断:当0°≤α<360°时,![]() 的大小有无变化?请仅就图2的情况给出证明.
的大小有无变化?请仅就图2的情况给出证明.
(3)问题解决
当△EDC旋转至A、D、E三点共线时,直接写出线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
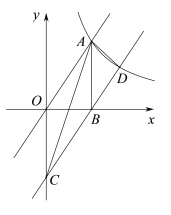
【题目】如图,正比例函数y1=kx与反比例函数![]() (x>0)交于点A(2,3),AB⊥x轴于点B,平移直线y1=kx使其经过点B,得到直线y2,y2与y轴交于点C,与
(x>0)交于点A(2,3),AB⊥x轴于点B,平移直线y1=kx使其经过点B,得到直线y2,y2与y轴交于点C,与![]() 交于点D.
交于点D.
(1)求正比例函数y1=kx及反比例函数![]() 的解析式;
的解析式;
(2)求点D的坐标;
(3)求△ACD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进甲、乙两种商品,甲种商品共用了2000元,乙种商品共用了2400元![]() 已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
已知乙种商品每件进价比甲种商品每件进价多8元,且购进的甲、乙两种商品件数相同.
![]() 求甲、乙两种商品的每件进价;
求甲、乙两种商品的每件进价;
![]() 该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变
该商场将购进的甲、乙两种商品进行销售,甲种商品的销售单价为60元,乙种商品的销售单价为88元,销售过程中发现甲种商品销量不好,商场决定:甲种商品销售一定数量后,将剩余的甲种商品按原销售单价的七折销售;乙种商品销售单价保持不变![]() 要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
要使两种商品全部售完后共获利不少于2460元,问甲种商品按原销售单价至少销售多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《人民日报》点赞湖北宜昌“智慧停车平台”.作为“全国智慧城市”试点,我市通过“互联网”、“大数据”等新科技,打造“智慧停车平台”,着力化解城市“停车难”问题.市内某智慧公共停车场的收费标准是:停车不超过![]() 分钟,不收费;超过
分钟,不收费;超过![]() 分钟,不超过
分钟,不超过![]() 分钟,计
分钟,计![]() 小时,收费
小时,收费![]() 元;超过
元;超过![]() 小时后,超过
小时后,超过![]() 小时的部分按每小时
小时的部分按每小时![]() 元收费(不足
元收费(不足![]() 小时,按
小时,按![]() 小时计).
小时计).
(1)填空:若市民张先生某次在该停车场停车![]() 小时
小时![]() 分钟,应交停车费________元.若李先生也在该停、车场停车,支付停车费
分钟,应交停车费________元.若李先生也在该停、车场停车,支付停车费![]() 元,则停车场按________小时(填整数)计时收费.
元,则停车场按________小时(填整数)计时收费.
(2)当![]() 取整数且
取整数且![]() 时,求该停车场停车费
时,求该停车场停车费![]() (单位:元)关于停车计时
(单位:元)关于停车计时![]() (单位:小时)的函数解析式.
(单位:小时)的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,按要求解答问题:
阅读理解:若p、q、m为整数,且三次方程![]() 有整数解c,则将c代入方程得:
有整数解c,则将c代入方程得:![]() ,移项得:
,移项得:![]() ,即有:
,即有:![]() ,由于
,由于![]() 与c及m都是整数,所以c是m的因数.
与c及m都是整数,所以c是m的因数.
上述过程说明:整数系数方程![]() 的整数解只可能是m的因数.
的整数解只可能是m的因数.
例如:方程![]() 中-2的因数为±1和±2,将它们分别代入方程
中-2的因数为±1和±2,将它们分别代入方程![]() 进行验证得:x=-2是该方程的整数解,-1、1、2不是方程的整数解.
进行验证得:x=-2是该方程的整数解,-1、1、2不是方程的整数解.
解决问题:
①根据上面的学习,请你确定方程![]() 的整数解只可能是哪几个整数?
的整数解只可能是哪几个整数?
②方程![]() 是否有整数解?若有,请求出其整数解;若没有,请说明理由.
是否有整数解?若有,请求出其整数解;若没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com