
【题目】如图,正比例函数y1=kx与反比例函数![]() (x>0)交于点A(2,3),AB⊥x轴于点B,平移直线y1=kx使其经过点B,得到直线y2,y2与y轴交于点C,与
(x>0)交于点A(2,3),AB⊥x轴于点B,平移直线y1=kx使其经过点B,得到直线y2,y2与y轴交于点C,与![]() 交于点D.
交于点D.
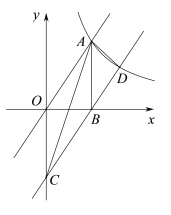
(1)求正比例函数y1=kx及反比例函数![]() 的解析式;
的解析式;
(2)求点D的坐标;
(3)求△ACD的面积.
【答案】(1)y1=![]() x,
x,![]() ;(2)D坐标为(
;(2)D坐标为(![]() ,
,![]() );(3)
);(3)![]() .
.
【解析】
(1)用待定系数法,即可求得;(2)y2由y1平移得到,所以设y2=![]() x+b,然后通过点B求出平移后的函数解析式,然后与
x+b,然后通过点B求出平移后的函数解析式,然后与![]() 联立,即可确定D的坐标;(3)通过D点坐标确定DE的长,用S△ACD=S△OCD面积相等,法求出OC的长,计算即可.
联立,即可确定D的坐标;(3)通过D点坐标确定DE的长,用S△ACD=S△OCD面积相等,法求出OC的长,计算即可.
解:(1)将点A(2,3)分别带入y1=kx、![]() 得3=2k、
得3=2k、![]() ,解得k=
,解得k=![]() ,m=6,
,m=6,
∴正比例函数y1=kx及反比例函数![]() 的解析式分别为y1=
的解析式分别为y1=![]() x、
x、![]() ;
;
(2)∵y2由y1平移得到,所以设y2=![]() x+b,
x+b,
∵AB⊥x轴,
∴B(2,0),将其带入y2=![]() x+b得b=-3,
x+b得b=-3,
∴y2=![]() x-3,
x-3,
解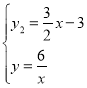 得
得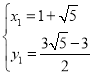 ,
,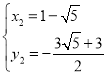 (舍),
(舍),
∴点D坐标为(![]() ,
,![]() );
);
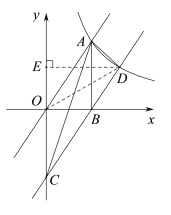
(3)如答图,连接OD,作DE⊥y轴于E,则DE=![]() ,
,
∵直线y1∥y2,
∴S△ACD=S△OCD=![]() ×OC×DE=
×OC×DE=![]() ×3×(
×3×(![]() )=
)=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,形如量角器的半圆O的直径DE-12cm,形如三角板的△ABC中,∠ACB=90°,tan∠ABC= ![]() ,BC=12cm半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上。设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.
,BC=12cm半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上。设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.

(1)点C到直线AB的距离为 ________cm;
(2)当t= ________(s)时,⊙O与AC所在直线第一次相切;当t=________(s)时,⊙O与AC所在直线第二次相切;
(3)当t为何值时,直线AB与半圆O所在的圆相切;
(4)当△ABC的一边所在直线与圆O相切时,若⊙O与△ABC有重叠部分,直接写出重叠部分的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中卷第九“勾股”章,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑,东西七里,南北九里,各中开门,出东门一十五里有木,问:出南门几何步而见木?”译文:“如图,今有一座长方形小城,东西向城墙长7里,南北向城墙长9里,各城墙正中均开一城门.走出东门15里处有棵大树,问走出南门多少步恰好能望见这棵树?”(注:1里=300步)你的计算结果是:出南门________步而见木.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是平行四边形,对角线
是平行四边形,对角线![]() 在
在![]() 轴正半轴上,位于第一象限的点
轴正半轴上,位于第一象限的点![]() 和第二象限的点
和第二象限的点![]() 分别在双曲线
分别在双曲线![]() 和
和![]() 的一个分支上,分别过点
的一个分支上,分别过点![]() 作
作![]() 轴的垂线段,垂足分别为点
轴的垂线段,垂足分别为点![]() 和
和![]() ,则以下结论:
,则以下结论:
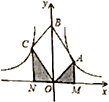
①![]() ; ②阴影部分面积是
; ②阴影部分面积是![]() ;
;
③当![]() 时,
时,![]() ; ④若
; ④若![]() 是菱形,则两双曲线既关于x轴对称,也关于y轴对称.
是菱形,则两双曲线既关于x轴对称,也关于y轴对称.
其中正确结论的个数是
A. ![]() 个B.
个B. ![]() 个C.
个C. ![]() 个D.
个D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论:①abc>0;②9a+3b+c<0;③c>﹣1;④关于x的方程ax2+bx+c=0(a≠0)有一个根为![]() ,其中正确结论的个数为( )
,其中正确结论的个数为( )
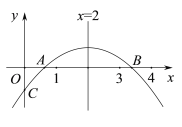
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某软件科技公司20人负责研发与维护游戏、网购、视频和送餐共4款软件.投入市场后,游戏软件的利润占这4款软件总利润的40%.如图是这4款软件研发与维护人数的扇形统计图和利润的条形统计图.
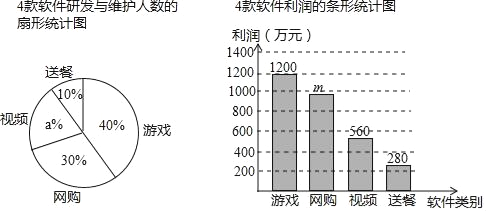
根据以上信息,网答下列问题
(1)直接写出图中a,m的值;
(2)分别求网购与视频软件的人均利润;
(3)在总人数和各款软件人均利润都保持不变的情况下,能否只调整网购与视频软件的研发与维护人数,使总利润增加60万元?如果能,写出调整方案;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() 和
和 ![]() ,与
,与![]() 轴交于另一点
轴交于另一点![]() ,顶点为
,顶点为![]() .
.
(1)求抛物线的解析式,并写出![]() 点的坐标;
点的坐标;
(2)如图,点![]() 分别在线段
分别在线段![]() 上(
上(![]() 点不与
点不与![]() 重合),且
重合),且![]() ,则
,则![]() 能否为等腰三角形?若能,求出
能否为等腰三角形?若能,求出![]() 的长;若不能,请说明理由;
的长;若不能,请说明理由;
(3)若点![]() 在抛物线上,且
在抛物线上,且![]() ,试确定满足条件的点
,试确定满足条件的点![]() 的个数.
的个数.
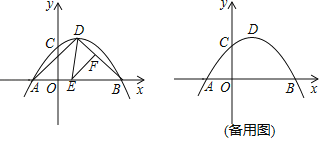
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将背面完全相同,正面上分别写有数字1,2,3,4的四张卡片混合后,嘉辉从中随机地抽取一张,把卡片上的数字作为被减数。将形状、大小完全相同,分别标有数字1,2,3的三个小球混合后,向东从中随机地抽取一个,把小球上的数字作为减数,然后计算出这两数的差。
(1)请你用画树状图或列表的方法,求这两数的差为0的概率;
(2)嘉辉与向东做游戏,规则是:若这两数的差为非负数,则嘉辉赢;否则,向东赢。你认为该游戏公平吗?请说明理由。如果不公平,请你修改游戏规则,使游戏公平。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com