
【题目】将背面完全相同,正面上分别写有数字1,2,3,4的四张卡片混合后,嘉辉从中随机地抽取一张,把卡片上的数字作为被减数。将形状、大小完全相同,分别标有数字1,2,3的三个小球混合后,向东从中随机地抽取一个,把小球上的数字作为减数,然后计算出这两数的差。
(1)请你用画树状图或列表的方法,求这两数的差为0的概率;
(2)嘉辉与向东做游戏,规则是:若这两数的差为非负数,则嘉辉赢;否则,向东赢。你认为该游戏公平吗?请说明理由。如果不公平,请你修改游戏规则,使游戏公平。
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,正比例函数y1=kx与反比例函数![]() (x>0)交于点A(2,3),AB⊥x轴于点B,平移直线y1=kx使其经过点B,得到直线y2,y2与y轴交于点C,与
(x>0)交于点A(2,3),AB⊥x轴于点B,平移直线y1=kx使其经过点B,得到直线y2,y2与y轴交于点C,与![]() 交于点D.
交于点D.
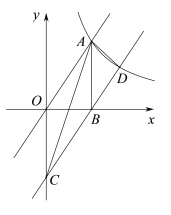
(1)求正比例函数y1=kx及反比例函数![]() 的解析式;
的解析式;
(2)求点D的坐标;
(3)求△ACD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
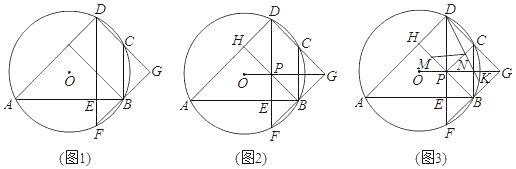
【题目】已知:四边形ABCD内接于⊙O,∠ADC=90°,DE⊥AB,垂足为点E,DE的锯长线交⊙O于点F,DC的延长线与FB的延长线交于点G.
(1)如图1,求证:GD=GF;
(2)如图2,过点B作BH⊥AD,垂足为点M,B交DF于点P,连接OG,若点P在线段OG上,且PB=PH,求∠ADF的大小;
(3)如图3,在(2)的条件下,点M是PH的中点,点K在![]() 上,连接DK,PC,D交PC点N,连接MN,若AB=12
上,连接DK,PC,D交PC点N,连接MN,若AB=12![]() ,HM+CN=MN,求DK的长.
,HM+CN=MN,求DK的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
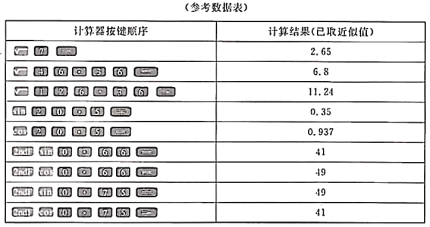
【题目】如图所示,一种适用于笔记本电脑的铝合金支架,边![]() ,
,![]() 可绕点
可绕点![]() 开合,在
开合,在![]() 边上有一固定点
边上有一固定点![]() ,支柱
,支柱![]() 可绕点
可绕点![]() 转动,边
转动,边![]() 上有六个卡孔,其中离点
上有六个卡孔,其中离点![]() 最近的卡孔为
最近的卡孔为![]() ,离点
,离点![]() 最远的卡孔为
最远的卡孔为![]() .当支柱端点
.当支柱端点![]() 放入不同卡孔内,支架的倾斜角发生变化.将电脑放在支架上,电脑台面的角度可达到六档调节,这样更有利于工作和身体健康.现测得
放入不同卡孔内,支架的倾斜角发生变化.将电脑放在支架上,电脑台面的角度可达到六档调节,这样更有利于工作和身体健康.现测得![]() 的长为
的长为![]() ,
,![]() 为
为![]() ,支柱
,支柱![]() 为
为![]() .
.

(1)当支柱的端点![]() 放在卡孔
放在卡孔![]() 处时,求
处时,求![]() 的度数;
的度数;
(2)当支柱的端点![]() 放在卡孔
放在卡孔![]() 处时,
处时,![]() ,若相邻两个卡孔的距离相同,求此间距.(结果精确到十分位)
,若相邻两个卡孔的距离相同,求此间距.(结果精确到十分位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,按要求解答问题:
阅读理解:若p、q、m为整数,且三次方程![]() 有整数解c,则将c代入方程得:
有整数解c,则将c代入方程得:![]() ,移项得:
,移项得:![]() ,即有:
,即有:![]() ,由于
,由于![]() 与c及m都是整数,所以c是m的因数.
与c及m都是整数,所以c是m的因数.
上述过程说明:整数系数方程![]() 的整数解只可能是m的因数.
的整数解只可能是m的因数.
例如:方程![]() 中-2的因数为±1和±2,将它们分别代入方程
中-2的因数为±1和±2,将它们分别代入方程![]() 进行验证得:x=-2是该方程的整数解,-1、1、2不是方程的整数解.
进行验证得:x=-2是该方程的整数解,-1、1、2不是方程的整数解.
解决问题:
①根据上面的学习,请你确定方程![]() 的整数解只可能是哪几个整数?
的整数解只可能是哪几个整数?
②方程![]() 是否有整数解?若有,请求出其整数解;若没有,请说明理由.
是否有整数解?若有,请求出其整数解;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形ABC的边长是2,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接MN,则在点M运动过程中,线段MN长度的最小值是( )

A. ![]() B. 1 C.
B. 1 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,点P是BC边上一点,连接AP,点E,F是AP上的两点,连接DE,BF,使得∠AED=∠ABC,∠ABF=∠BPF.
求证:(1)△ABF≌△DAE;
(2)DE=BF+EF.

查看答案和解析>>
科目:初中数学 来源: 题型:
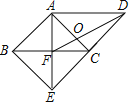
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,过点
,过点![]() 作边
作边![]() 的垂线
的垂线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,点
,点![]() 是垂足,连接
是垂足,连接![]() 、
、![]() ,
,![]() 交
交![]() 于点
于点![]() .则下列结论:①四边形
.则下列结论:①四边形![]() 是正方形;②
是正方形;②![]() ;③
;③![]() ;④
;④![]() ,正确的个数是( )
,正确的个数是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两地间的直线公路长为![]() 千米.一辆轿车和一辆货车分别沿该公路从甲、乙两地以各自的速度匀速相向而行,货车比轿车早出发
千米.一辆轿车和一辆货车分别沿该公路从甲、乙两地以各自的速度匀速相向而行,货车比轿车早出发![]() 小时,途中轿车出现了故障,停下维修,货车仍继续行驶.
小时,途中轿车出现了故障,停下维修,货车仍继续行驶.![]() 小时后轿车故障被排除,此时接到通知,轿车立刻掉头按原路原速返回甲地(接到通知及掉头时间不计).最后两车同时到达甲地,已知两车距各自出发地的距离
小时后轿车故障被排除,此时接到通知,轿车立刻掉头按原路原速返回甲地(接到通知及掉头时间不计).最后两车同时到达甲地,已知两车距各自出发地的距离![]() (千米)与轿车所用的时间
(千米)与轿车所用的时间![]() (小时)的关系如图所示,请结合图象解答下列问题:
(小时)的关系如图所示,请结合图象解答下列问题:
(1)货车的速度是_______千米/小时;轿车的速度是_______千米/小时;![]() 值为_______.
值为_______.
(2)求轿车距其出发地的距离![]() (千米)与所用时间
(千米)与所用时间![]() (小时)之间的函数关系式并写出自变量
(小时)之间的函数关系式并写出自变量![]() 的取值范围;
的取值范围;
(3)请直接写出货车出发多长时间两车相距![]() 千米.
千米.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com