
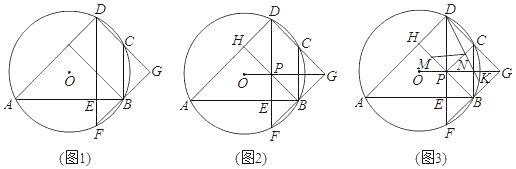
【题目】已知:四边形ABCD内接于⊙O,∠ADC=90°,DE⊥AB,垂足为点E,DE的锯长线交⊙O于点F,DC的延长线与FB的延长线交于点G.
(1)如图1,求证:GD=GF;
(2)如图2,过点B作BH⊥AD,垂足为点M,B交DF于点P,连接OG,若点P在线段OG上,且PB=PH,求∠ADF的大小;
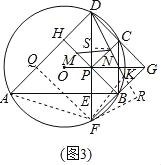
(3)如图3,在(2)的条件下,点M是PH的中点,点K在![]() 上,连接DK,PC,D交PC点N,连接MN,若AB=12
上,连接DK,PC,D交PC点N,连接MN,若AB=12![]() ,HM+CN=MN,求DK的长.
,HM+CN=MN,求DK的长.
【答案】(1)见解析;(2)∠ADF=45°;(3)![]() .
.
【解析】
(1)利用“同圆中,同弧所对的圆周角相等”可得∠A=∠GFD,由“等角的余角相等”可得∠A=∠GDF,等量代换得∠GDF=∠GFD,根据“三角形中,等角对等边”得GD=GF;
(2)连接OD、OF,由△DPH≌△FPB可得:∠GBH=90°,由四边形内角和为360°可得:∠G=90°,即可得:∠ADF=45°;
(3)由等腰直角三角形可得AH=BH=12,DF=AB=12![]() ,由四边形ABCD内接于⊙O,可得:∠BCG=45°=∠CBG,GC=GB,可证四边形CDHP是矩形,令CN=m,利用勾股定理可求得m=2,过点N作NS⊥DP于S,连接AF,FK,过点F作FQ⊥AD于点Q,过点F作FR⊥DK交DK的延长线于点R,通过构造直角三角形,应用解直角三角形方法球得DK.
,由四边形ABCD内接于⊙O,可得:∠BCG=45°=∠CBG,GC=GB,可证四边形CDHP是矩形,令CN=m,利用勾股定理可求得m=2,过点N作NS⊥DP于S,连接AF,FK,过点F作FQ⊥AD于点Q,过点F作FR⊥DK交DK的延长线于点R,通过构造直角三角形,应用解直角三角形方法球得DK.
解:(1)证明:∵DE⊥AB
∴∠BED=90°
∴∠A+∠ADE=90°
∵∠ADC=90°
∴∠GDF+∠ADE=90°
∴∠A=∠GDF
∵![]()
∴∠A=∠GFD
∴∠GDF=∠GFD
∴GD=GF
(2)连接OD、OF
∵OD=OF,GD=GF
∴OG⊥DF,PD=PF
在△DPH和△FPB中
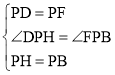
∴△DPH≌△FPB(SAS)
∴∠FBP=∠DHP=90°
∴∠GBH=90°
∴∠DGF=360°﹣90°﹣90°﹣90°=90°
∴∠GDF=∠DFG=45°
∴∠ADF=45°
(3)在Rt△ABH中,∵∠BAH=45°,AB=12![]()
∴AH=BH=12
∴PH=PB=6
∵∠HDP=∠HPD=45°
∴DH=PH=6
∴AD=12+6=18,PN=HM=![]() PH=3,PD=6
PH=3,PD=6![]()
∵∠BFE=∠EBF=45°
∴EF=BE
∵∠DAE=∠ADE=45°
∴DE=AE
∴DF=AB=12![]()
∵四边形ABCD内接于⊙O
∴∠DAB+∠BCD=180°
∴∠BCD=135°
∴∠BCG=45°=∠CBG
∴GC=GB
又∵∠CGP=∠BGP=45°,GP=GP
∴△GCP≌△GBP(SAS)
∴∠PCG=∠PBG=90°
∴∠PCD=∠CDH=∠DHP=90°
∴四边形CDHP是矩形
∴CD=HP=6,PC=DH=6,∠CPH=90°
令CN=m,则PN=6﹣m,MN=m+3
在Rt△PMN中,∵PM2+PN2=MN2
∴32+(6﹣m)2=(m+3)2,解得m=2
∴PN=4
过点N作NS⊥DP于S,
在Rt△PSN中,PS=SN=2![]()
DS=6![]() ﹣2
﹣2![]() =4
=4![]()
![]()
连接AF,FK,过点F作FQ⊥AD于点Q,过点F作FR⊥DK交DK的延长线于点R
在Rt△DFQ中,FQ=DQ=12
∴AQ=18﹣12=6
∴tan![]()
∵四边形AFKD内接于⊙O,
∴∠DAF+∠DKF=180°
∴∠DAF=180°﹣∠DKF=∠FKR
在Rt△DFR中,∵DF=![]()
∴![]()
在Rt△FKR中,∵FR=![]() tan∠FKR=2
tan∠FKR=2
∴KR=![]()
∴DK=DR﹣KR=![]() .
.




 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中卷第九“勾股”章,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑,东西七里,南北九里,各中开门,出东门一十五里有木,问:出南门几何步而见木?”译文:“如图,今有一座长方形小城,东西向城墙长7里,南北向城墙长9里,各城墙正中均开一城门.走出东门15里处有棵大树,问走出南门多少步恰好能望见这棵树?”(注:1里=300步)你的计算结果是:出南门________步而见木.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() 和
和 ![]() ,与
,与![]() 轴交于另一点
轴交于另一点![]() ,顶点为
,顶点为![]() .
.
(1)求抛物线的解析式,并写出![]() 点的坐标;
点的坐标;
(2)如图,点![]() 分别在线段
分别在线段![]() 上(
上(![]() 点不与
点不与![]() 重合),且
重合),且![]() ,则
,则![]() 能否为等腰三角形?若能,求出
能否为等腰三角形?若能,求出![]() 的长;若不能,请说明理由;
的长;若不能,请说明理由;
(3)若点![]() 在抛物线上,且
在抛物线上,且![]() ,试确定满足条件的点
,试确定满足条件的点![]() 的个数.
的个数.
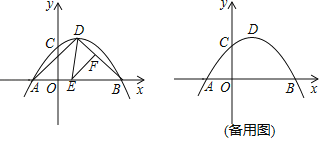
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=-x2+1,下列结论:
①抛物线开口向上;
②抛物线与x轴交于点(-1,0)和点(1,0);
③抛物线的对称轴是y轴;
④抛物线的顶点坐标是(0,1);
⑤抛物线y=-x2+1是由抛物线y=-x2向上平移1个单位得到的.
其中正确的个数有( )
A. 5个B. 4个C. 3个
D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将背面完全相同,正面上分别写有数字1,2,3,4的四张卡片混合后,嘉辉从中随机地抽取一张,把卡片上的数字作为被减数。将形状、大小完全相同,分别标有数字1,2,3的三个小球混合后,向东从中随机地抽取一个,把小球上的数字作为减数,然后计算出这两数的差。
(1)请你用画树状图或列表的方法,求这两数的差为0的概率;
(2)嘉辉与向东做游戏,规则是:若这两数的差为非负数,则嘉辉赢;否则,向东赢。你认为该游戏公平吗?请说明理由。如果不公平,请你修改游戏规则,使游戏公平。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国著名的数学家华罗庚曾巧解开立方的智力题:问题:59319是一个整数的立方,求这个整数?
解答:因为:10<![]() <100,所以:
<100,所以:![]() 是两位整数;
是两位整数;
因为:整数59319的末位上的数字是9,而整数0~9的立方中,只有93=729的末位数字是9,
所以:![]() 的末位数字是9;又因为划去59319的后面三位319得到59,而3<
的末位数字是9;又因为划去59319的后面三位319得到59,而3<![]() <4,
<4,
所以![]() 的十位数字是3;因此
的十位数字是3;因此![]() =39.
=39.
应用:已知2(2x﹣2)3+221184=0,其中x是整数.则x的值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com