
【题目】如图,形如量角器的半圆O的直径DE-12cm,形如三角板的△ABC中,∠ACB=90°,tan∠ABC= ![]() ,BC=12cm半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上。设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.
,BC=12cm半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上。设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.

(1)点C到直线AB的距离为 ________cm;
(2)当t= ________(s)时,⊙O与AC所在直线第一次相切;当t=________(s)时,⊙O与AC所在直线第二次相切;
(3)当t为何值时,直线AB与半圆O所在的圆相切;
(4)当△ABC的一边所在直线与圆O相切时,若⊙O与△ABC有重叠部分,直接写出重叠部分的面积。
【答案】(1)6;(2)1,7;(3)t为4秒或16秒;(4)6π+9![]() cm2
cm2
【解析】
(1)由tan∠ABC=![]() , 可知∠ABC=30°,再根据在直角三角形中,30°所对的直角边等于斜边的一半,可知CF=
, 可知∠ABC=30°,再根据在直角三角形中,30°所对的直角边等于斜边的一半,可知CF=![]() AC=6;
AC=6;
(2)由题意可知,DE为⊙O的直径,即OE=6,OC=8,所以EC=2,⊙O与AC所在的直线第一次相切,即点C与点E重合,也就是t=1时;DC=DE+EC=14,⊙O与AC所在的直线第二次相切,即点D与点E重合时,也就是t=7;
(3)此题有两种情况:第一种情况,直线AB与半圆O相切,即过点O的半径与AB所在的直线垂直,也就是CF⊥AB,即点O与点C重合时,也就是t=4;第二种情况,直线Ab与半圆O相切,即点O运动到点B的右侧时,即过点O的半径与AB的延长线垂直,此时OC=24,也就是t=(24+8)÷2=16;
(4)此题有三种情况:第一种情况是⊙O与AC第一次相切时,此时⊙O与△ABC没有重叠部分;第二种情况是O与AB相切时,此时重叠的部分为O的四分之一,即为9πcm2;第三种情况是O与AC第二次相切时,此时⊙O的直径DE与△ABC的边BC重合,重叠部分的面积等于△BOG与扇形GOC的和,即6π+9![]() cm2
cm2
(1)由tan∠ABC=![]() , 可知∠ABC=30°,再根据在直角三角形中,30°所对的直角边等于斜边的一半,可知CF=
, 可知∠ABC=30°,再根据在直角三角形中,30°所对的直角边等于斜边的一半,可知CF=![]() AC=6;
AC=6;
(2)由题意可知,DE为⊙O的直径,即OE=6,OC=8,所以EC=2,⊙O与AC所在的直线第一次相切,即点C与点E重合,也就是t=1时;DC=DE+EC=14,⊙O与AC所在的直线第二次相切,即点D与点E重合时,也就是t=7;
(3)解:如图2,过C作CF⊥AB于F , 同理得:OF=6,
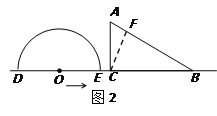
当直线AB与半圆O所在的圆相切时,又∵圆心O到AB的距离为6,半圆的半径为6,
且圆心O又在直线BC上,∴O与C重合,即当O点运动到C点时,半圆O与△ABC的边AB相切,
此时,点O运动了8cm , 所求运动时间t=8÷2=4;
如图3,当点O运动到B点的右侧时,且OB=12,过O作OQ⊥AB , 交直线AB于Q ,

在Rt△QOB中,∠OBQ=30°,则OQ= ![]() OB=6,即OQ与半圆O所在的圆相切,此时点O运动了12+12+8=32cm , 所求运动时间t=32÷2=16,
OB=6,即OQ与半圆O所在的圆相切,此时点O运动了12+12+8=32cm , 所求运动时间t=32÷2=16,
综上所述,当t为4秒或16秒时,直线AB与半圆O所在的圆相切
(4)解:重叠部分的面积为/span>9πcm2或(6π+9 ![]() )cm2 . 有两种情况:
)cm2 . 有两种情况:
①当半圆O与AB边相切于F时,如图1,重叠部分的面积S= ![]() π×62=9π;
π×62=9π;
②当半圆O与AC相切于C时,如图4,连接OG ,
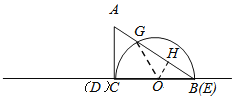
∵BC=DE=12,∴C与D重合,E与B重合,∵OG=OB , ∴∠ABC=∠OGB=30°,
∴∠COG=60°.过O作OH⊥AB于H , ∵OB=6,∴OH= ![]() OB=3,
OB=3,
由勾股定理得:BH=3 ![]() ,∴BG=2BH=6
,∴BG=2BH=6 ![]() ,此时重叠部分的面积S=
,此时重叠部分的面积S= ![]() +
+ ![]() ×6
×6 ![]() ×3=6π+9
×3=6π+9 ![]() ;
;
综上所述,重叠部分的面积为9πcm2或(6π+9 ![]() )cm2
)cm2
圆的综合题
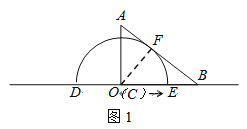
解:(1)如图1,过C作CF⊥AB于F ,
Rt△BCF中,∵tan∠ABC= ![]() ∴∠ABC=30°,BC=12,
∴∠ABC=30°,BC=12,
∴CF= ![]() BC=6,故答案为:6
BC=6,故答案为:6
 ;
;
(2)∵DE=12,∴OE=OD=6,∵OC=8,∴EC=8-6=2,∴t=2÷2=1,
∴当t=1s时,⊙O与AC所在直线第一次相切;∴DC=8+6=14,∴t=14÷2=7,
∴当t=7s时,⊙O与AC所在直线第二次相切;故答案为:1,7


科目:初中数学 来源: 题型:
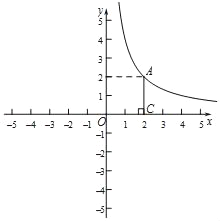
【题目】如图,在平面直角坐标系xOy中,函数y=![]() (x>0)的图象经过点A,作AC⊥x轴于点C.
(x>0)的图象经过点A,作AC⊥x轴于点C.
(1)求k的值;
(2)直线y=ax+b(a≠0)图象经过点A交x轴于点B,且OB=2AC.求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着城际铁路的开通,从甲市到乙市的高铁里程比快里程缩短了90千米,运行时间减少了8小时,已知甲市到乙市的普快列车里程为1220千米,高铁平均时速是普快平均时速的2.5倍.
(1)求高铁列车的平均时速;
(2)若从甲市到乙市途经丙市,且从甲市到丙市的高铁里程为780千米.某日王老师要从甲市去丙市参加14:00召开的会议,如果他买了当日10:00从甲市到丙市的高铁票,而且从丙市高铁站到会议地点最多需要0.5小时.试问在高铁列车准点到达的情况下,王老师能否在开会之前赶到会议地点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一台起重机,他的机身高AC为21m,吊杆AB长为36m,吊杆与水平线的夹角∠BAD可从30°升到80°.求这台起重机工作时,吊杆端点B离地面CE的最大高度和离机身AC的最大水平距离(结果精确到0.1m). (参考数据:sin80°≈0.98,cos80°≈0.17,tan33°≈5.67,![]() ≈1.73)
≈1.73)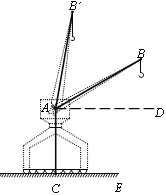
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图中是小明完成的一道作业题,请你参考小明的解答方法解答下面的问题:
小明的作业
计算:(-4)7×0.257
解:(-4)7×0.257=(-4×0.25)7
=(-1)7
=-1
(1)计算①82018×(-0.125)2018② ![]()
(2)看2·4n·16n=219 , 求n的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2018年梧州市体育中考中,每名学生需考3个项目(包括2个必考项目与1个选考项目)每个项目20分,总分60分.其中必考项目为:跳绳和实心球;选考项目:A篮球、B足球、C排球、D立定跳远、E50米跑,F女生800米跑或男生1000米跑.某兴趣小组随机对同学们的选考项目做了调查,根据调查结果绘制了两幅不完整的条形统计图与扇形统计图.结合图中信息,回答下列问题:
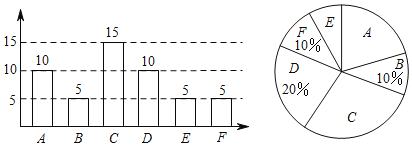
(1)在这次调查中,一共调查了 名学生,扇形统计图中C对应的圆心角的度数为 ;
(2)在本次调查的必考项目的众数是 ;(填A、B、C、D、E、F选项)
(3)选考项目包括球类与非球类,请用树状图或列表法求甲、乙两名同学都选球类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠A=30°,以点B为圆心,适当长为半径的画弧,分别交BA,BC于点M、N;再分别以点M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D,则下列说法中不正确的是()
MN的长为半径画弧,两弧交于点P,作射线BP交AC于点D,则下列说法中不正确的是()

A. BP是∠ABC的平分线B. AD=BDC. ![]() D. CD=
D. CD=![]() BD
BD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正比例函数y1=kx与反比例函数![]() (x>0)交于点A(2,3),AB⊥x轴于点B,平移直线y1=kx使其经过点B,得到直线y2,y2与y轴交于点C,与
(x>0)交于点A(2,3),AB⊥x轴于点B,平移直线y1=kx使其经过点B,得到直线y2,y2与y轴交于点C,与![]() 交于点D.
交于点D.
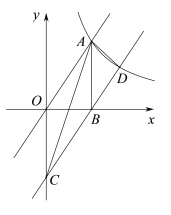
(1)求正比例函数y1=kx及反比例函数![]() 的解析式;
的解析式;
(2)求点D的坐标;
(3)求△ACD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com