
【题目】如图,一台起重机,他的机身高AC为21m,吊杆AB长为36m,吊杆与水平线的夹角∠BAD可从30°升到80°.求这台起重机工作时,吊杆端点B离地面CE的最大高度和离机身AC的最大水平距离(结果精确到0.1m). (参考数据:sin80°≈0.98,cos80°≈0.17,tan33°≈5.67,![]() ≈1.73)
≈1.73)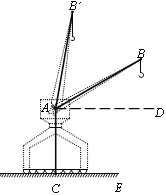
【答案】吊杆端点B离地面CE的最大高度为56.3cm,离机身AC的最大水平距离为31.1cm
【解析】
试题当∠BAD=30°时,吊杆端点B离机身AC的水平距离最大;
当∠B’AD=80°时,吊杆端点B’离地面CE的高度最大.
试题解析:当∠BAD=30°时,吊杆端点B离机身AC的水平距离最大;
当∠B’AD=80°时,吊杆端点B’离地面CE的高度最大.
作BF⊥AD于F,BG⊥CE于G,交AD于F’ .
在Rt△BAF中,cos∠BAF=![]() ,
,
∴AF=AB·cos∠BAF=40×cos30°≈34.6(cm).
在Rt△B’AF’中,sin∠BAF’=![]() ,
,
∴B’F’=AB’·sin∠B’AF’=40×sin80°≈39.2(cm).
∴B’G=B’F +F’G≈39.2+21=60.2(cm).
答:吊杆端点B离地面CE的最大高度约为60.2cm,离机身AC的最大水平距离约34.6cm.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(生活观察)甲、乙两人买菜,甲习惯买一定质量的菜,乙习惯买一定金额的菜,两人每次买菜的单价相同,例如:
菜价 | ||
质量 | 金额 | |
甲 |
|
|
乙 |
|
|
菜价 | ||
质量 | 金额 | |
甲 |
| ____元 |
乙 | ____千克 |
|
(1)完成上表;
(2)计算甲两次买菜的均价和乙两次买菜的均价.(均价![]() 总金额总质量)
总金额总质量)
(数学思考)设甲每次买质量为![]() 千克的菜,乙每次买金额为
千克的菜,乙每次买金额为![]() 元的菜,两次的单价分别是
元的菜,两次的单价分别是![]() 元
元![]() 千克、
千克、![]() 元
元![]() 千克,用含有
千克,用含有![]() 、
、![]() 、
、![]() 、
、![]() 的式子,分别表示出甲、乙两次买菜的均价
的式子,分别表示出甲、乙两次买菜的均价![]() 、
、![]() .比较
.比较![]() 、
、![]() 的大小,并说明理由.
的大小,并说明理由.
(知识迁移)某船在相距为![]() 的甲、乙两码头间往返航行一次,在没有水流时,船的速度为
的甲、乙两码头间往返航行一次,在没有水流时,船的速度为![]() 所需时间为:如果水流速度为
所需时间为:如果水流速度为![]() 时(
时(![]() ),船顺水航行速度为(
),船顺水航行速度为(![]() ),逆水航行速度为(
),逆水航行速度为(![]() ),所需时间为
),所需时间为![]() 请借鉴上面的研究经验,比较
请借鉴上面的研究经验,比较![]() 、
、![]() 的大小,并说明理由.
的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c图象的一部分,且抛物线的对称轴为x=﹣1,那么下列说法正确的是( )
①b2>4ac;②abc>0;③2a+b=0;④a+b+c>0;⑤a﹣b+c<0.

A. ①②③④B. ②④⑤C. ②③④D. ①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形OABC的边OC、OA分别位于x、y轴上,点A(0,﹣4)、B(6,﹣4)、C(6,0),抛物线y=ax2+bx经过点O和点C,顶点M(3,﹣![]() ),点N是抛物线上一动点,直线MN交直线AB于点E,交y轴于F,△A′EF是将△AEF沿直线MN翻折后的图形.
),点N是抛物线上一动点,直线MN交直线AB于点E,交y轴于F,△A′EF是将△AEF沿直线MN翻折后的图形.
(1)求抛物线的解析式;
(2)当四边AEA′F是正方形时,求点N的坐标.
(3)连接CA′,求CA′的最小值.
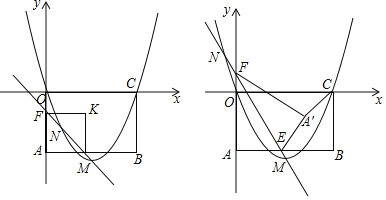
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一组数:1,1,2,3,5,8,13,…,其中从第三个数起,每一个数都等于它前面两个数的和.现以这组数中的各个数作为正方形的边长值构造正方形,再分别依次从左到右取2个、3个、4个、5个…正方形拼成如上长方形,若按此规律继续作长方形,则序号为⑦的长方形周长是 .
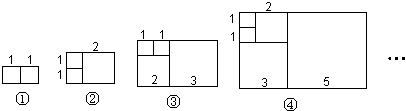
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,形如量角器的半圆O的直径DE-12cm,形如三角板的△ABC中,∠ACB=90°,tan∠ABC= ![]() ,BC=12cm半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上。设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.
,BC=12cm半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上。设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.

(1)点C到直线AB的距离为 ________cm;
(2)当t= ________(s)时,⊙O与AC所在直线第一次相切;当t=________(s)时,⊙O与AC所在直线第二次相切;
(3)当t为何值时,直线AB与半圆O所在的圆相切;
(4)当△ABC的一边所在直线与圆O相切时,若⊙O与△ABC有重叠部分,直接写出重叠部分的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘海轮位于灯塔P的东北方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处。
(1)求海轮从A处到B处的途中与灯塔P之间的最短距离(结果保留根号);
(2)若海轮以每小时30海里的速度从A处到B处,试判断海轮能否在5小时内到达B处,并说明理由。
(参考数据:![]() )
)
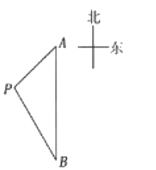
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是平行四边形,对角线
是平行四边形,对角线![]() 在
在![]() 轴正半轴上,位于第一象限的点
轴正半轴上,位于第一象限的点![]() 和第二象限的点
和第二象限的点![]() 分别在双曲线
分别在双曲线![]() 和
和![]() 的一个分支上,分别过点
的一个分支上,分别过点![]() 作
作![]() 轴的垂线段,垂足分别为点
轴的垂线段,垂足分别为点![]() 和
和![]() ,则以下结论:
,则以下结论:
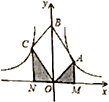
①![]() ; ②阴影部分面积是
; ②阴影部分面积是![]() ;
;
③当![]() 时,
时,![]() ; ④若
; ④若![]() 是菱形,则两双曲线既关于x轴对称,也关于y轴对称.
是菱形,则两双曲线既关于x轴对称,也关于y轴对称.
其中正确结论的个数是
A. ![]() 个B.
个B. ![]() 个C.
个C. ![]() 个D.
个D. ![]() 个
个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com