
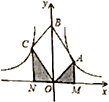
【题目】如图,![]() 是平行四边形,对角线
是平行四边形,对角线![]() 在
在![]() 轴正半轴上,位于第一象限的点
轴正半轴上,位于第一象限的点![]() 和第二象限的点
和第二象限的点![]() 分别在双曲线
分别在双曲线![]() 和
和![]() 的一个分支上,分别过点
的一个分支上,分别过点![]() 作
作![]() 轴的垂线段,垂足分别为点
轴的垂线段,垂足分别为点![]() 和
和![]() ,则以下结论:
,则以下结论:
①![]() ; ②阴影部分面积是
; ②阴影部分面积是![]() ;
;
③当![]() 时,
时,![]() ; ④若
; ④若![]() 是菱形,则两双曲线既关于x轴对称,也关于y轴对称.
是菱形,则两双曲线既关于x轴对称,也关于y轴对称.
其中正确结论的个数是
A. ![]() 个B.
个B. ![]() 个C.
个C. ![]() 个D.
个D. ![]() 个
个
【答案】B
【解析】
作AE⊥y轴于点E,CF⊥y轴于点F,根据平行四边形的性质得S△AOB=S△COB,利用三角形面积公式得到AE=CF,则有OM=ON,再利用反比例函数k的几何意义和三角形面积公式得到S△AOM=![]() |k1|=
|k1|=![]() OMAM,S△CON=
OMAM,S△CON=![]() |k2|=
|k2|=![]() ONCN,所以有
ONCN,所以有![]() ;由S△AOM=
;由S△AOM=![]() |k1|,S△CON=
|k1|,S△CON=![]() |k2|,得到S阴影部分=S△AOM+S△CON=
|k2|,得到S阴影部分=S△AOM+S△CON=![]() (|k1|+|k2|)=
(|k1|+|k2|)=![]() (k1-k2);当∠AOC=90°,得到四边形OABC是矩形,由于不能确定OA与OC相等,则不能判断△AOM≌△CNO,所以不能判断AM=CN,则不能确定|k1|=|k2|;若OABC是菱形,根据菱形的性质得OA=OC,可判断Rt△AOM≌Rt△CNO,则AM=CN,所以|k1|=|k2|,即k1=-k2,根据反比例函数的性质得两双曲线既关于x轴对称,也关于y轴对称.
(k1-k2);当∠AOC=90°,得到四边形OABC是矩形,由于不能确定OA与OC相等,则不能判断△AOM≌△CNO,所以不能判断AM=CN,则不能确定|k1|=|k2|;若OABC是菱形,根据菱形的性质得OA=OC,可判断Rt△AOM≌Rt△CNO,则AM=CN,所以|k1|=|k2|,即k1=-k2,根据反比例函数的性质得两双曲线既关于x轴对称,也关于y轴对称.
作AE⊥y轴于E,CF⊥y轴于F,如图,
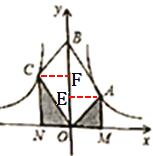
∵四边形OABC是平行四边形,
∴S△AOB=S△COB
∴AE=CF,
∴OM=ON,
∵S△AOM=![]() |k1|=
|k1|=![]() OMAM,S△CON=
OMAM,S△CON=![]() |k2|=
|k2|=![]() ONCN,
ONCN,
∴![]() ,故①正确;
,故①正确;
∵S△AOM=![]() |k1|,S△CON=
|k1|,S△CON=![]() |k2|,
|k2|,
∴S阴影部分=S△AOMspan>+S△CON=![]() (|k1|+|k2|),
(|k1|+|k2|),
而k1>0,k2<0,
∴S阴影部分=![]() (k1-k2),故②正确;
(k1-k2),故②正确;
当∠AOC=90°,
∴四边形OABC是矩形,
∴不能确定OA与OC相等,
而OM=ON,
∴不能判断△AOM≌△CNO,
∴不能判断AM=CN,
∴不能确定|k1|=|k2|,故③错误;
若OABC是菱形,则OA=OC,
而OM=ON,
∴Rt△AOM≌Rt△CNO,
∴AM=CN,
∴|k1|=|k2|,
∴k1=-k2,
∴两双曲线既关于x轴对称,也关于y轴对称,故④正确.
故选B.


科目:初中数学 来源: 题型:
【题目】如图,一台起重机,他的机身高AC为21m,吊杆AB长为36m,吊杆与水平线的夹角∠BAD可从30°升到80°.求这台起重机工作时,吊杆端点B离地面CE的最大高度和离机身AC的最大水平距离(结果精确到0.1m). (参考数据:sin80°≈0.98,cos80°≈0.17,tan33°≈5.67,![]() ≈1.73)
≈1.73)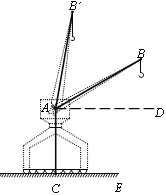
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=4,O为矩形ABCD的中心,以D为圆心1为半径作⊙D,P为⊙D上的一个动点,连接AP,OP,则△AOP面积的最大值为_____.
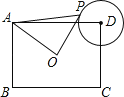
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() 抛物线
抛物线![]() 经过点
经过点![]() 、
、![]() .
.
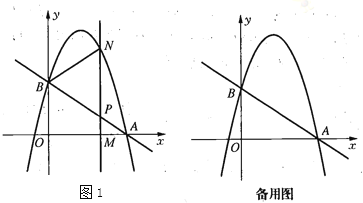
(1)求点![]() 的坐标和抛物线的解析式.
的坐标和抛物线的解析式.
(2)![]() 为
为![]() 轴上一个动点,过点
轴上一个动点,过点![]() 垂直于
垂直于![]() 轴的直线与直线
轴的直线与直线![]() 和抛物线分别交于点
和抛物线分别交于点![]() 、
、![]() .
.
①点![]() 在线段
在线段![]() 上运动,若以
上运动,若以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的坐标;
的坐标;
②点![]() 在
在![]() 轴上自由运动,若三个点
轴上自由运动,若三个点![]() 、
、![]() 、
、![]() 中恰有一点是其他两点所连线段的中点(三点重合除外),则称
中恰有一点是其他两点所连线段的中点(三点重合除外),则称![]() 、
、![]() 、
、![]() 三点为“共谐点”.请直接写出使得
三点为“共谐点”.请直接写出使得![]() 、
、![]() 、
、![]() 三点成为“共谐点”的
三点成为“共谐点”的![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正比例函数y1=kx与反比例函数![]() (x>0)交于点A(2,3),AB⊥x轴于点B,平移直线y1=kx使其经过点B,得到直线y2,y2与y轴交于点C,与
(x>0)交于点A(2,3),AB⊥x轴于点B,平移直线y1=kx使其经过点B,得到直线y2,y2与y轴交于点C,与![]() 交于点D.
交于点D.
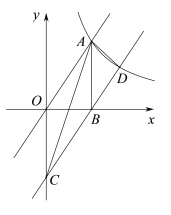
(1)求正比例函数y1=kx及反比例函数![]() 的解析式;
的解析式;
(2)求点D的坐标;
(3)求△ACD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一笔直的海岸线l上有相距2km的A,B两个观测站,B站在A站的正东方向上,从A站测得船C在北偏东60°的方向上,从B站测得船C在北偏东30°的方向上,则船C到海岸线l的距离为多少千米?(参考数据:![]() ≈1.732,结果保留小数点后一位)
≈1.732,结果保留小数点后一位)
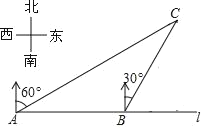
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一种适用于笔记本电脑的铝合金支架,边![]() ,
,![]() 可绕点
可绕点![]() 开合,在
开合,在![]() 边上有一固定点
边上有一固定点![]() ,支柱
,支柱![]() 可绕点
可绕点![]() 转动,边
转动,边![]() 上有六个卡孔,其中离点
上有六个卡孔,其中离点![]() 最近的卡孔为
最近的卡孔为![]() ,离点
,离点![]() 最远的卡孔为
最远的卡孔为![]() .当支柱端点
.当支柱端点![]() 放入不同卡孔内,支架的倾斜角发生变化.将电脑放在支架上,电脑台面的角度可达到六档调节,这样更有利于工作和身体健康.现测得
放入不同卡孔内,支架的倾斜角发生变化.将电脑放在支架上,电脑台面的角度可达到六档调节,这样更有利于工作和身体健康.现测得![]() 的长为
的长为![]() ,
,![]() 为
为![]() ,支柱
,支柱![]() 为
为![]() .
.

(1)当支柱的端点![]() 放在卡孔
放在卡孔![]() 处时,求
处时,求![]() 的度数;
的度数;
(2)当支柱的端点![]() 放在卡孔
放在卡孔![]() 处时,
处时,![]() ,若相邻两个卡孔的距离相同,求此间距.(结果精确到十分位)
,若相邻两个卡孔的距离相同,求此间距.(结果精确到十分位)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com