
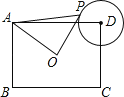
【题目】如图,在矩形ABCD中,AB=3,BC=4,O为矩形ABCD的中心,以D为圆心1为半径作⊙D,P为⊙D上的一个动点,连接AP,OP,则△AOP面积的最大值为_____.
【答案】![]()
【解析】
当P点移动到平行于OA且与⊙D相切时,△AOP面积的最大,由于P为切点,得出MP垂直与切线,进而得出PM⊥AC,根据勾股定理先求得AC的长,进而求得OA的长,根据△ADM∽△ACD,求得DM的长,从而求得PM的长,最后根据三角形的面积公式即可求得;
解:当P点移动到过点P的直线平行于OA且与⊙D相切时,△AOP面积的最大,如图,
∵过P的直线是⊙D的切线,
∴DP垂直于切线,
延长PD交AC于M,则DM⊥AC,
∵在矩形ABCD中,AB=3,BC=4,
∴AC=![]() ,
,
∴OA=![]() ,
,
∵∠AMD=∠ADC=90°,∠DAM=∠CAD,
∴△ADM∽△ACD,
∴![]() ,
,
∵AD=4,CD=3,AC=5,
∴DM=![]() ,
,
∴PM=PD+DM=1+![]() =
=![]() ,
,
∴△AOP的最大面积=![]() OAPM=
OAPM=![]() ×
×![]() ×
×![]() =
=![]() ,
,
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c图象的一部分,且抛物线的对称轴为x=﹣1,那么下列说法正确的是( )
①b2>4ac;②abc>0;③2a+b=0;④a+b+c>0;⑤a﹣b+c<0.

A. ①②③④B. ②④⑤C. ②③④D. ①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
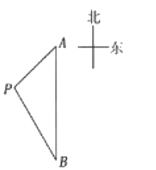
【题目】如图,一艘海轮位于灯塔P的东北方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向上的B处。
(1)求海轮从A处到B处的途中与灯塔P之间的最短距离(结果保留根号);
(2)若海轮以每小时30海里的速度从A处到B处,试判断海轮能否在5小时内到达B处,并说明理由。
(参考数据:![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为改善教学条件,学校准备对现有多媒体设备进行升级改造,已知购买3个键盘和1个鼠标需要190元;购买2个键盘和3个鼠标需要220元;
(1)求键盘和鼠标的单价各是多少元?
(2)经过与经销商洽谈,键盘打八折,鼠标打八五折.若学校计划购买键盘和鼠标共50件,且总费用不超过1820元,则最多可购买键盘多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中卷第九“勾股”章,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑,东西七里,南北九里,各中开门,出东门一十五里有木,问:出南门几何步而见木?”译文:“如图,今有一座长方形小城,东西向城墙长7里,南北向城墙长9里,各城墙正中均开一城门.走出东门15里处有棵大树,问走出南门多少步恰好能望见这棵树?”(注:1里=300步)你的计算结果是:出南门________步而见木.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,以点(3,-5)为圆心,r为半径的圆上有且仅有两点到x轴所在直线的距离等于1,则圆的半径r的取值范围是 ( )
A.r>4 B.0<r<6 C.4≤r<6 D.4<r<6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是平行四边形,对角线
是平行四边形,对角线![]() 在
在![]() 轴正半轴上,位于第一象限的点
轴正半轴上,位于第一象限的点![]() 和第二象限的点
和第二象限的点![]() 分别在双曲线
分别在双曲线![]() 和
和![]() 的一个分支上,分别过点
的一个分支上,分别过点![]() 作
作![]() 轴的垂线段,垂足分别为点
轴的垂线段,垂足分别为点![]() 和
和![]() ,则以下结论:
,则以下结论:
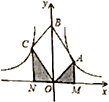
①![]() ; ②阴影部分面积是
; ②阴影部分面积是![]() ;
;
③当![]() 时,
时,![]() ; ④若
; ④若![]() 是菱形,则两双曲线既关于x轴对称,也关于y轴对称.
是菱形,则两双曲线既关于x轴对称,也关于y轴对称.
其中正确结论的个数是
A. ![]() 个B.
个B. ![]() 个C.
个C. ![]() 个D.
个D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某软件科技公司20人负责研发与维护游戏、网购、视频和送餐共4款软件.投入市场后,游戏软件的利润占这4款软件总利润的40%.如图是这4款软件研发与维护人数的扇形统计图和利润的条形统计图.
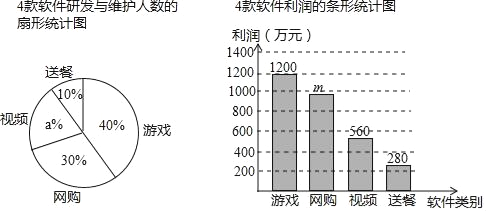
根据以上信息,网答下列问题
(1)直接写出图中a,m的值;
(2)分别求网购与视频软件的人均利润;
(3)在总人数和各款软件人均利润都保持不变的情况下,能否只调整网购与视频软件的研发与维护人数,使总利润增加60万元?如果能,写出调整方案;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=-x2+1,下列结论:
①抛物线开口向上;
②抛物线与x轴交于点(-1,0)和点(1,0);
③抛物线的对称轴是y轴;
④抛物线的顶点坐标是(0,1);
⑤抛物线y=-x2+1是由抛物线y=-x2向上平移1个单位得到的.
其中正确的个数有( )
A. 5个B. 4个C. 3个
D. 2个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com