
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 利用反例对(1)进行判断;根据等腰梯形的对角线相等和三角形中位线性质、菱形的判定方法可对(2)进行判断;根据弦对两条弧可对(3)进行判断;根据正九边形的性质和余弦的定义可对(4)解析判断.
解答 解:有理数乘以无理数不一定是无理数,若0乘以π得0,所以(1)错误;
顺次联结等腰梯形各边中点所得的四边形是菱形,所以(2)正确;
在同圆中,相等的弦所对的弧对应相等,所以(3)错误;
如果正九边形的半径为a,那么边心距为a•cos20°,所以(4)错误.
故选A.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式. 有些命题的正确性是用推理证实的,这样的真命题叫做定理.


 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:填空题
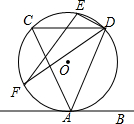 如图,直线AB与⊙O相切于点A,弦CD∥AB,E,F为圆上的两点,且∠CDE=∠ADF,若⊙O的直径为5,CD=4,则弦EF的长为2$\sqrt{5}$.
如图,直线AB与⊙O相切于点A,弦CD∥AB,E,F为圆上的两点,且∠CDE=∠ADF,若⊙O的直径为5,CD=4,则弦EF的长为2$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,小明在大楼30米高即(PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚处的俯角为60°.已知该山坡的坡度i(即tan∠ABC)为1:$\sqrt{3}$,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC,则A到BC的距离为10$\sqrt{3}$米.
如图,小明在大楼30米高即(PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚处的俯角为60°.已知该山坡的坡度i(即tan∠ABC)为1:$\sqrt{3}$,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC,则A到BC的距离为10$\sqrt{3}$米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
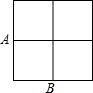 如图,在2×2的正方形网格中四个小正方形的顶点叫格点,已经取定格点A和B,在余下的格点中任取一点C,使△ABC为直角三角形的概率是$\frac{4}{7}$.
如图,在2×2的正方形网格中四个小正方形的顶点叫格点,已经取定格点A和B,在余下的格点中任取一点C,使△ABC为直角三角形的概率是$\frac{4}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
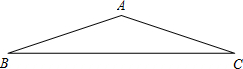 如图,已知在△ABC中,AB=AC,tan∠B=$\frac{1}{3}$,将△ABC翻折,使点C与点A重合,折痕DE交边BC于点D,交边AC于点E,那么$\frac{BD}{DC}$的值为
如图,已知在△ABC中,AB=AC,tan∠B=$\frac{1}{3}$,将△ABC翻折,使点C与点A重合,折痕DE交边BC于点D,交边AC于点E,那么$\frac{BD}{DC}$的值为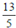 .
.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com