
【题目】如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=![]() ,∠BAD=60°,且AB>
,∠BAD=60°,且AB>![]() .
.
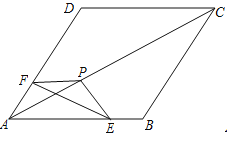
(1)求∠EPF的大小;
(2)若AP=8,求AE+AF的值;
(3)若△EFP的三个顶点E,F,P分别在线段AB,AD,AC上运动,请直接写出AP长的最大值和最小值.
【答案】(1)120°;(2)![]() ;(3)AP的最大值为12,AP的最小值为6.
;(3)AP的最大值为12,AP的最小值为6.
【解析】
试题分析:(1)如图,过点P作PG⊥EF于G,已知PE=PF=6,EF=![]() ,根据等腰三角形的性质可得FG=EG=
,根据等腰三角形的性质可得FG=EG=![]() ,∠FPG=∠EPG=
,∠FPG=∠EPG=![]() .在Rt△FPG中,由sin∠FPG=
.在Rt△FPG中,由sin∠FPG=![]() 可求得∠FPG=60°,所以∠EPF=2∠FPG=120°.(2)作PM⊥AB于M,PN⊥AD于N,根据菱形的性质可得∠DAC=∠BAC,AM=AN,PM=PN,再利用HL证明Rt△PME≌Rt△PNF,即可得NF=ME.又因AP=10,
可求得∠FPG=60°,所以∠EPF=2∠FPG=120°.(2)作PM⊥AB于M,PN⊥AD于N,根据菱形的性质可得∠DAC=∠BAC,AM=AN,PM=PN,再利用HL证明Rt△PME≌Rt△PNF,即可得NF=ME.又因AP=10,![]() ,所以AM= AN =APcos30°=
,所以AM= AN =APcos30°=![]() =
=![]() .所以AE+AF=(AM+ME)+(AN-NF)=AM+AN=
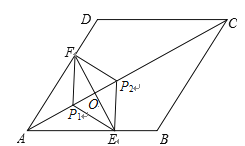
.所以AE+AF=(AM+ME)+(AN-NF)=AM+AN=![]() .(3)如图,当△EFP的三个顶点E,F,P分别在线段AB,AD,AC上运动时,点P在
.(3)如图,当△EFP的三个顶点E,F,P分别在线段AB,AD,AC上运动时,点P在![]() ,
,![]() 之间运动,易知
之间运动,易知![]() ,
,![]() ,所以AP的最大值为12,AP的最小值为6.
,所以AP的最大值为12,AP的最小值为6.
试题解析:(1)如图,过点P作PG⊥EF于G.
∵PE=PF=6,EF=![]() ,
,
∴FG=EG=![]() ,∠FPG=∠EPG=
,∠FPG=∠EPG=![]() .
.
在Rt△FPG中,sin∠FPG=![]() .
.
∴∠FPG=60°,
∴∠EPF=2∠FPG=120°.
(2)作PM⊥AB于M,PN⊥AD于N.
∵AC为菱形ABCD的对角线,
∴∠DAC=∠BAC,AM=AN,PM=PN.
在Rt△PME和Rt△PNF 中,PM=PN,PE=PF,
∴Rt△PME≌Rt△PNF
∴NF=ME.
又AP=10,![]() ,
,
∴AM= AN =APcos30°=![]() =
=![]() .
.
∴AE+AF=(AM+ME)+(AN-NF)=AM+AN=![]() .
.

(3) 如图,当△EFP的三个顶点E,F,P分别在线段AB,AD,AC上运动时,点P在![]() ,
,![]() 之间运动,易知
之间运动,易知![]() ,
,![]() ,
,
∴AP的最大值为12,AP的最小值为6.


科目:初中数学 来源: 题型:
【题目】列方程解实际问题
华联商厦进货员在广州发现一种饰品,预计能畅销市场,就用8000元购进所有饰品,每件按58元很快卖完. 由于销路很好,又在上海用13200元购进,这次比在广州多进了100件,单价比广州贵了10%,但商厦仍按原售价销售,最后剩下的15件按八折销售,很快售完,问该商厦这两批饰品生意共赚了多少 ?(不考虑其它因素)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
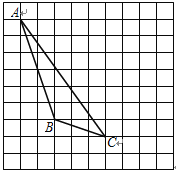
(1)画出△ABC向右平移4个单位后得到的△A1B1C1;
(2)图中AC与A1C1的关系是: _____________.
(3)画出△ABC的AB边上的高CD;垂足是D;
(4)图中△ABC的面积是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列不等式变形中,错误的是( )
A. 若 a≤b,则 a+c≤b+cB. 若 a+c≤b+c,则 a≤b
C. 若 a≤b,则 ac2≤bc2D. 若 ac2≤bc2,则 a≤b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A. 对角线互相平分的四边形是平行四边形
B. 对角线相等的四边形是矩形
C. 对角线互相垂直的四边形是菱形
D. 对角线互相垂直的四边形是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com