
【题目】如图,一次函数与反比例函数y= ![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点. 
(1)求反比例函数的解析式;
(2)点P是x轴上的一动点,试确定点P使PA+PB最小,并求出点P的坐标.
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )
A.“射击运动员射击一次,命中靶心”是必然事件
B.不可能事件发生的概率为0
C.随机事件发生的概率为 ![]()
D.投掷一枚质地均匀的硬币100次,正面朝上的次数一定为50次
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,反比例函数y= ![]() (x>0)的图象经过点A(2
(x>0)的图象经过点A(2 ![]() ,1),射线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D.
,1),射线AB与反比例函数图象交于另一点B(1,a),射线AC与y轴交于点C,∠BAC=75°,AD⊥y轴,垂足为D. 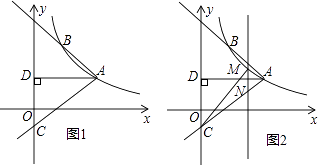
(1)求k的值;
(2)求tan∠DAC的值及直线AC的解析式;
(3)如图2, 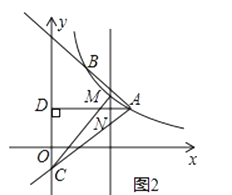
M是线段AC上方反比例函数图象上一动点,过M作直线l⊥x轴,与AC相交于点N,连接CM,求△CMN面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AD平分∠BAC交⊙O于点D,过点D作DE∥BC交AC的延长线于点E. 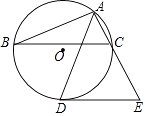
(1)试判断DE与⊙O的位置关系,并证明你的结论;
(2)若∠E=60°,⊙O的半径为5,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确的结论有(填序号). 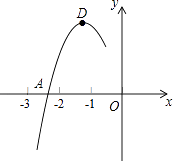
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2016年龙岩市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A.平均数为160
B.中位数为158
C.众数为158
D.方差为20.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4. 如图2,正方形ABCD顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.
如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈D;若第二次掷得2,就从D开始顺时针连续跳2个边长,落到圈B;…
设游戏者从圈A起跳.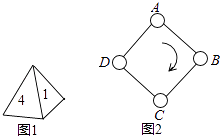
(1)嘉嘉随机掷一次骰子,求落回到圈A的概率P1;
(2)淇淇随机掷两次骰子,用列表法求最后落回到圈A的概率P2 , 并指出她与嘉嘉落回到圈A的可能性一样吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知双曲线y= ![]() (x>0),直线l1:y﹣
(x>0),直线l1:y﹣ ![]() =k(x﹣
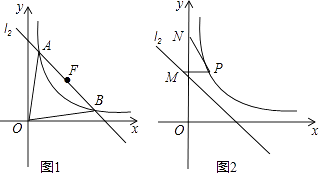
=k(x﹣ ![]() )(k<0)过定点F且与双曲线交于A,B两点,设A(x1 , y1),B(x2 , y2)(x1<x2),直线l2:y=﹣x+
)(k<0)过定点F且与双曲线交于A,B两点,设A(x1 , y1),B(x2 , y2)(x1<x2),直线l2:y=﹣x+ ![]() .
.
(1)若k=﹣1,求△OAB的面积S;
(2)若AB= ![]()
![]() ,求k的值;
,求k的值;
(3)设N(0,2 ![]() ),P在双曲线上,M在直线l2上且PM∥x轴,问在第二象限内是否存在一点Q,使得四边形QMPN是周长最小的平行四边形?若存在,请求出Q点的坐标.
),P在双曲线上,M在直线l2上且PM∥x轴,问在第二象限内是否存在一点Q,使得四边形QMPN是周长最小的平行四边形?若存在,请求出Q点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D为AB上一点,E为BC上一点,且AC=CD=BD=BE,∠A=50°,则∠CDE的度数为( ) 
A.50°
B.51°
C.51.5°
D.52.5°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com