
【题目】如图所示,已知正△ABC中射线CM⊥AB于F,射线BA绕B顺时针旋转,旋转后的射线记作a,同时线段AB所在直线绕A顺时针旋转,旋转后的直线记作直线l,当直线l旋转的角度是射线a旋转角度的4倍时,直线l于射线CM相交于E,与射线a相交于D,且∠D=30°.
(1)求射线a的旋转角是多少度;
(2)求证:DE=AB;
(3)探索:线段DE,EF,DB的数量关系.

【答案】(1)10°;(2)证明见解析;(3)DB=EF+![]() DE.
DE.
【解析】
试题分析:(1)根据三角形的一个外角等于与它不相邻的两内角的和,直线a,l的旋转角的关系建立方程4α=30°+α即可;
(2)由∠BCE=∠D=30°,判断出点B,C,D,E四点共圆,再判断出∠EBD=∠BDC,即可;
(3)判断出△BDE≌△ECA,再代换即可.
试题解析:(1)设直线l旋转角为α,
∴∠ABD=α
∵射线l旋转的角度是射线a旋转角度的4倍,
∴∠BAE=4α,
∵∠BAE=∠ABD+∠D,
∴4α=α+30°,
∴α=10°,
射线a的旋转角是10°;
(2)连接BE,

在正△ABC中,CF⊥AB,
∴∠BCE=30°,
∵∠D=30°,
∴∠BCE=∠D=30°,
∴点B,C,D,E四点共圆(线段同侧的两点对线段的张角相等,则这两点以及线段的两个端点共圆)
∵CE⊥AB,AF=BF,
∴EA=EB,
∴∠EBA=∠BAE=40°,
∴∠EBD=50°,∠EBC=100°,
∴∠EDC=80°,
∴∠BDC=50°
∴∠EBD=∠BDC,
∴DE=BC,
∵BC=AB,
∴DE=AB,
(3)∵∠BAE=40°,
∴∠AEC=50°,
∵∠ABE=40°,∠ABD=10°,
∴∠EBD=∠AEC=50°
∵∠BDE=∠ACE=30°,DE=AC,
∴△BDE≌△ECA,
∴BD=EC=EF+FC=EF+![]() AB=EF+
AB=EF+![]() DE.
DE.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
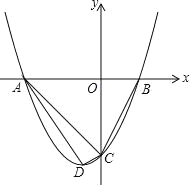
【题目】已知:二次函数y=ax2+bx+c的图象与x轴相交于A(-4,0),B(2,0)两点,与y轴相交于点C(0,-4),点D为抛物线的顶点.
(1)求二次函数的解析式;
(2)求S△ABC:S△ACD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b的图象与反比例函数y2=![]() 的图象交于A(m,3),B(-3,n)两点.
的图象交于A(m,3),B(-3,n)两点.
(1)求一次函数的解析式;
(2)观察函数图象,直接写出关于x的不等式![]() >kx+b的解集.
>kx+b的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解放中学为了了解学生对新闻、体育、动画、娱乐四类电视节目的喜爱程度,随机抽取了部分学生进行调查(每人限选1项),现将调查结果绘制成如下两幅不完整的统计图,根据图中所给的信息解答下列问题.
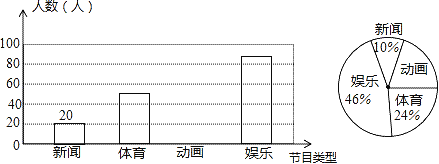
(1)喜爱动画的学生人数和所占比例分别是多少?
(2)请将条形统计图补充完整;
(3)若该校共有学生1000人,依据以上图表估计该校喜欢体育的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
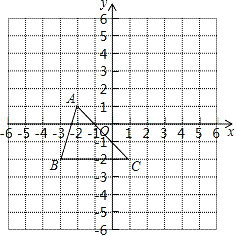
【题目】如图所示,三角形ABC(记作△ABC)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(﹣2,1),B(﹣3,﹣2),C(1,﹣2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到A1B1C1.
(1)在图中画出△A1B1C1;
(2)点A1,B1,C1的坐标分别为 、 、 ;
(3)若y轴有一点P,使△PBC与△ABC面积相等,求出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场在销售旺季临近时,某品牌的童装销售价格呈上升趋势,假如这种童装开始时的售价为每件20元,并且每周(7天)涨价2元,从第6周开始,保持每件30元的稳定价格销售,直到11周结束,该童装不再销售.
(1)请建立销售价格y(元)与周次x之间的函数关系;
(2)若该品牌童装于进货当周售完,且这种童装每件进价z(元)与周次x之间的关系为z=-![]() (x-8)2+12,1≤x≤11,且x为整数,那么该品牌童装在第几周售出后,每件获得利润最大?并求最大利润为多少?
(x-8)2+12,1≤x≤11,且x为整数,那么该品牌童装在第几周售出后,每件获得利润最大?并求最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,如果∠B﹣2∠C=90°﹣∠C,那么△ABC是( )
A. 直角三角形
B. 钝角三角形
C. 锐角三角形
D. 锐角三角形或钝角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com