
【题目】已知:如图,AB∥CD,E是AB的中点,CE=DE.求证:
(1)∠AEC=∠BED;
(2)AC=BD.
【答案】
(1)证明:∵AB∥CD,
∴∠AEC=∠ECD,∠BED=∠EDC,
∵CE=DE,
∴∠ECD=∠EDC,
∴∠AEC=∠BED
(2)证明:∵E是AB的中点,
∴AE=BE,
在△AEC和△BED中,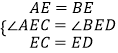 ,
,
∴△AEC≌△BED(SAS),
∴AC=BD.
【解析】第一小题考查平行线的性质,两平行线内错角相等.∠AEC=∠ECD,∠BED=∠EDC.根据等腰三角形的性质得到∠ECD=∠EDC,根据等价关系得∠AEC=∠BED.
第二小题考查全等三角形的判断与证明,由第一问得到的∠AEC=∠BED做为已知条件,因为E是AB的中点,得到AE=BE.根据判定定理(SAS)
在△AEC和△BED中,A E= BE,∠ A E C = ∠ B E D, E C = E D.得到△AEC≌△BED.两三角形全等则对应边相等得到AC=BD.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
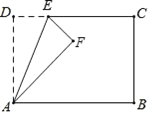
【题目】如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查活动中适合使用全面调查的是( )
A.某种品牌插座的使用寿命;
B.全国植树节中栽植树苗的成活率;
C.了解某班同学课外阅读经典情况;
D.调查“厉害了,我的国”大型记录电影在线收视率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )
A.5 ![]()
B.25
C.10 ![]() +5
+5
D.35
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB交x轴于点A(4,0),交y轴于点B,交反比例函数y=![]() (k≠0)于点P(第一象限),若点P的纵坐标为2,且tan∠BAO=1
(k≠0)于点P(第一象限),若点P的纵坐标为2,且tan∠BAO=1
(1)求出反比例函数y=![]() (k≠0)的解析式;
(k≠0)的解析式;
(2)过线段AB上一点C作x轴的垂线,交反比例函数y=![]() (k≠0)于点D,连接PD,当△CDP为等腰三角形时,求点C的坐标.
(k≠0)于点D,连接PD,当△CDP为等腰三角形时,求点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校射击队从甲、乙、丙、丁四人中选拔一人参加市运会射击比赛.在选拔赛中,每人射击10次,他们10次成绩的平均数及方差如下表所示.
甲 | 乙 | 丙 | 丁 | |
平均数/环 | 9.7 | 9.5 | 9.5 | 9.7 |
方差/环2 | 5.1 | 4.7 | 4.5 | 4.5 |
请你根据表中数据选一人参加比赛,最合适的人选是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com