
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CM将△CMA折叠,使点A落在点D处,若CD恰好与MB垂直,且BC=4,则△ABC 的面积为_____________.

【答案】![]()
【解析】由CM为Rt△ABC斜边AB上的中线,根据直角三角形斜边上的中线性质得CM=MB=AM,再根据折叠的性质得到MD=MA,∠DMC=∠AMC,则MD=MC,由于CD⊥MB于H,
根据等腰三角形的性质有MH平分∠DMC,即∠BMC=∠BMD,可得∠DMC=2∠BMC,∠AMC=2∠BMC,利用平角的定义可计算出∠BMC=60°,则△BMC为等边三角形,易得
∠B=60°,∠A=30°,所以AC=![]() BC=4
BC=4![]() ,然后根据三角形面积公式进行计算.
,然后根据三角形面积公式进行计算.
如图,
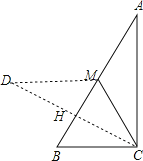
∵CM为Rt△ABC斜边AB上的中线,
∴CM=MB=AM,
∵沿△ABC的中线CM将△CMA折叠,点A落在点D处,
∴MD=MA,∠DMC=∠AMC,
∴MD=MC,
∵CD⊥MB于H,
∴MH平分∠DMC,即∠BMC=∠BMD,
∴∠DMC=2∠BMC,
∴∠AMC=2∠BMC,
∵∠BMC+∠AMC=180°,
∴∠BMC=60°,
∴△BMC为等边三角形,
∴∠B=60°,
∴∠A=30°,
∴AC=![]() BC=4
BC=4![]() ,
,
∴S△ABC=![]() ACBC=
ACBC=![]() ×4
×4![]() ×4=8
×4=8![]() .
.
故答案为8![]() .
.


科目:初中数学 来源: 题型:
【题目】填写下表
序号 |
| 1 | 2 | … |
① |
| 5 |
| … |
② |
| 2 |
| … |
③ |
|
| 4 | … |
随着![]() 值的逐渐变大,回答下列问题
值的逐渐变大,回答下列问题
(1)当![]() 时,这三个代数式中 的值最小;
时,这三个代数式中 的值最小;
(2)你预计代数式的值最先超过1000的是代数式 ,此时![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
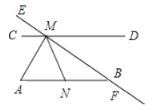
【题目】如图,∠CME+∠ABF=180°,MA平分∠CMN.若∠MNA=62°,求∠A的度数.根据提示将解题过程补充完整.
解:因为∠ABM+∠ABF=180°,
又因为∠CME+∠ABF=180°(已知),
所以∠ABM=∠CME
所以AB∥CD,理由:( )
所以∠CMN+( )=180°,
理由:(__________________________)
因为∠MNA=62°,
所以∠CMN=( )
因为MA平分∠CMN,
所以∠AMC=![]() ∠CMN =( ).(角平分线的定义)
∠CMN =( ).(角平分线的定义)
因为AB∥CD,
所以∠A=∠AMC=( )理由:(__________________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
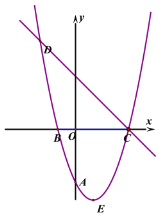
【题目】已知抛物线![]() 经过A(0,-3),B(-1,0),且抛物线对称轴为直线
经过A(0,-3),B(-1,0),且抛物线对称轴为直线![]() ,E
,E
是抛物线的顶点。
(1)求抛物线的解析式以及顶点坐标E。
(2)在![]() 轴上是否存在点P,使得
轴上是否存在点P,使得![]() 周长最短,若存在,请求出P点坐标,若不存在,请说
周长最短,若存在,请求出P点坐标,若不存在,请说
明理由。
(3)直线![]() 与抛物线交于C、D两点,Q是直线DC下方抛物线上的一点,是否存在点Q
与抛物线交于C、D两点,Q是直线DC下方抛物线上的一点,是否存在点Q
使得![]() 的面积最大,若存在请求出最大面积,若不存在,请说明理由。
的面积最大,若存在请求出最大面积,若不存在,请说明理由。
(4)抛物线上是否存在点M,使得![]() 是直角三角形,若存在,直接写出M点坐标,若不
是直角三角形,若存在,直接写出M点坐标,若不
存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列两个三角形中,一定全等的是()
A. 两个等边三角形
B. 有一个角是![]() ,腰相等的两个等腰三角形
,腰相等的两个等腰三角形
C. 有一条边相等,有一个内角相等的两个等腰三角形
D. 有一个角是![]() ,底相等的两个等腰三角形
,底相等的两个等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
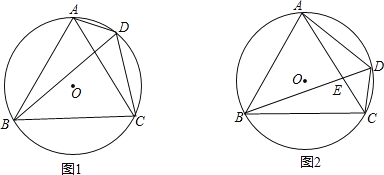
【题目】已知:等边三角形△ABC内接于⊙O,点D在![]() 上,连接AD、CD、BD,
上,连接AD、CD、BD,
(1)如图1,求证:∠ADB=∠BDC=60°;
(2)如图2,若BD=3CD,求证:AE=2CE;
(3)在(2)的条件下,连接OE,若BE=14,求线段OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店以每箱60元新进一批苹果共400箱,为计算总重量,从中任选30箱苹果称重,发现每箱苹果重量都在10千克左右,现以10千克为标准,超过10千克的数记为正数,不足10千克的数记为负数,将称重记录如下:

(1)求30箱苹果的总重量
(2)若每千克苹果的售价为10元,则卖完这批苹果共获利多少元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,三角形△ABC为等腰直角三角形,AC=BC,BC交x轴于点D.
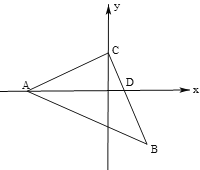
(1)若A(-4,0),C(0,2),求点B的坐标;
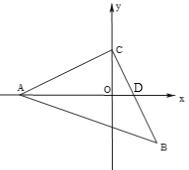
(2)若∠EDB=∠ADC,问∠ADE与∠CAD满足怎样的关系?并证明.
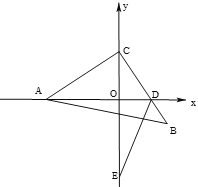
(3)若AD平分∠BAC,A(-4,0),D(m,0),B的纵坐标为n,试探究m、n之间满足怎样的关系?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com