
【题目】已知:等边三角形△ABC内接于⊙O,点D在![]() 上,连接AD、CD、BD,
上,连接AD、CD、BD,
(1)如图1,求证:∠ADB=∠BDC=60°;
(2)如图2,若BD=3CD,求证:AE=2CE;
(3)在(2)的条件下,连接OE,若BE=14,求线段OE的长.
【答案】(1)证明见解析;(2)证明见解析.(3)![]()
【解析】
(1)根据同弧所对的圆周角相等,推出∠BDC=∠BAC=60°,∠ADC=∠ACB=60°即可解决问题.
(2)如图2中,在BD上截取DH=DC,作EN⊥AD,EM⊥CD垂足分别为N、M.由△ACD≌△BCH推出BD=DA+DC,结合条件推出AD=2DC,再根据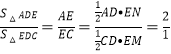 ,即可证明.
,即可证明.
(3)如图3中,连接AO,由此AO交BC于M,连接OE,作EN⊥BC于N,设OE=x.用x表示BN、EN,在Rt△EBN中,利用勾股定理列出方程即可.
(1)证明:如图1中,
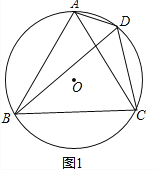
∵△ABC是等边三角形,
∴∠BAC=∠ACB=60°,
∵∠BDC=∠BAC,∠ADC=∠ACB,
∴∠ADB=∠BDC=60°.
(2)如图2中,在BD上截取DH=DC,作EN⊥AD,EM⊥CD垂足分别为N、M.
∵∠HDC=60°,DH=DC,
∴△DHC是等边三角形,
∴HC=DC,∠CHD=60°,
∴∠BCA=∠HCD=60°,
∴∠BCH=∠ACD,
在△BCH和△ACD中,
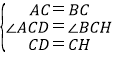 ,
,
∴△ACD≌△BCH,
∴BH=AD,
∴BD=BH+HD=AD+CD.
∵BD=3CD,
∴3CD=AD+CD,
∴AD=2CD,
∵∠ADB=∠BDC,EN⊥DA,EM⊥DC,
∴EN=EM,
∵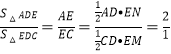 ,
,
∴AE=2CE.
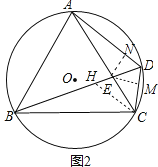
(3)如图3中,连接AO,由此AO交BC于M,连接OE,作EN⊥BC于N,设OE=x.
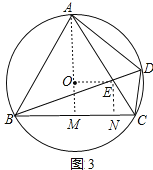
∵O是等边三角形的外心,
∴OA=2OM,∵AE=2EC,
∴![]() ,
,
∴OE∥CM,
∵AM⊥BC,
∴AO⊥OE,
∵∠OAE=![]() ∠BAC=30°,
∠BAC=30°,
∴AE=2x,EC=x,CN=![]() x,BN=
x,BN=![]() x,EN=
x,EN=![]() x
x
在Rt△BNE中,∵BE2=BN2+EN2,
∴142=(![]() x)2+(
x)2+(![]() x)2,
x)2,
∴x2=28,
∵x>0,
∴x=2![]() .
.
∴OE=2![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,CD⊥AB于点D,点E在CD上,下列四个条件:①AD=ED;②∠A=∠BED;③∠C=∠B;④AC=EB,将其中两个作为条件,不能判定△ADC≌△EDB的是
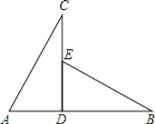
A.①②B.①④C.②③D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上两点间的距离等于这两点所对应的数的差的绝对值.例:如图所示,点![]() 在数轴上分别对应的数为
在数轴上分别对应的数为![]() ,则
,则![]() 两点间的距离表示为
两点间的距离表示为![]() .
.
![]()
根据以上知识解题:
(1)若数轴上两点![]() 表示的数分别为
表示的数分别为![]() 、-1,
、-1,
①![]() 之间的距离可用含
之间的距离可用含![]() 的式子表示为 ;
的式子表示为 ;
②若该两点之间的距离为2,那么![]() 值为 .
值为 .
(2)![]() 的最小值为 ,此时
的最小值为 ,此时![]() 可以取的整数值是 .
可以取的整数值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CM将△CMA折叠,使点A落在点D处,若CD恰好与MB垂直,且BC=4,则△ABC 的面积为_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知含字母m,n的代数式是:![]() .
.
(1)化简这个代数式.
(2)小明取m,n互为倒数的一对数值代入化简的代数式中,恰好计算得代数式的值等于0.那么小明所取的字母n的值等于多少?
(3)聪明的小智从化简的代数式中发现,只要字母n取一个固定的数,无论字母m取何数,代数式的值恒为一个不变的数,那么小智所取的字母n的值是多少呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
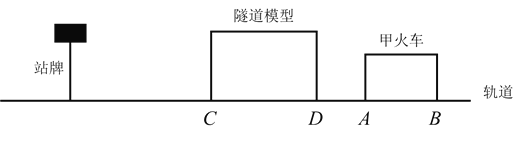
【题目】小明有一套火车玩具,有两列火车、一副轨道、一个隧道模型及一个站牌.特别之处:隧道模型也可以像火车一样移动,当火车头进入隧道一瞬间会响起音乐,当火车完全穿过隧道的一瞬间音乐会结束.已知甲火车长![]() 厘米,甲乙两列火车的速度均为
厘米,甲乙两列火车的速度均为![]() 厘米/秒,轨道长
厘米/秒,轨道长![]() 米.
米.
(1)将轨道围成一个圆圈,将甲、乙两列火车紧挨站牌放置,车头方向相反,同时启动,到两车相撞用时![]() 秒,求乙火车的长度?
秒,求乙火车的长度?
(2)在(1)的条件下,乙火车穿过静止的隧道音乐响起了![]() 秒,求隧道的长度;
秒,求隧道的长度;
(3)在(1)(2)的条件下,轨道铺成一条直线,把隧道模型、甲火车依次放在站牌的右侧,站牌静止不动,甲火车头与隧道相距![]() (即
(即![]() ).当甲火车向左运动,隧道模型以不变的速度运动,音乐却响了
).当甲火车向左运动,隧道模型以不变的速度运动,音乐却响了![]() 秒;当音乐结束的一瞬间,甲火车头
秒;当音乐结束的一瞬间,甲火车头![]() 与站牌相距乙火车车身的长度,请同学们思考一下,以站牌所在地为原点建立数轴,你能确定甲火车、隧道在运动前的位置吗?如果可以,请画出数轴并标出
与站牌相距乙火车车身的长度,请同学们思考一下,以站牌所在地为原点建立数轴,你能确定甲火车、隧道在运动前的位置吗?如果可以,请画出数轴并标出![]() 运动前的位置.
运动前的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在双曲线y=![]() (x>0)上,点C在双曲线y=
(x>0)上,点C在双曲线y=![]() (x>0)上,若AC∥y轴,BC∥x轴,且AC=BC,则AB等于( )
(x>0)上,若AC∥y轴,BC∥x轴,且AC=BC,则AB等于( )
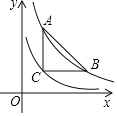
A. ![]() B. 2
B. 2![]() C. 4 D. 3
C. 4 D. 3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:
①二次函数y=ax2+bx+c的最小值为﹣4a;
②若﹣1≤x2≤4,则0≤y2≤5a;
③若y2>y1,则x2>4;
④一元二次方程cx2+bx+a=0的两个根为﹣1和![]()
其中正确结论的个数是( )
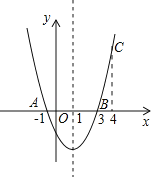
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com