
【题目】如图,CD⊥AB于点D,点E在CD上,下列四个条件:①AD=ED;②∠A=∠BED;③∠C=∠B;④AC=EB,将其中两个作为条件,不能判定△ADC≌△EDB的是
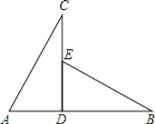
A.①②B.①④C.②③D.②④
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】乘法公式的探究及应用.
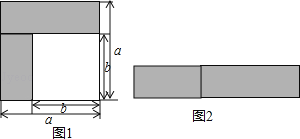
(1)如图1,阴影部分的面积是 (写成平方差的形式);
(2)如图2,若将阴影部分裁剪后重新拼成一个长方形,它的宽是 长是 ,面积可表示为 (写成多项式乘法的形式).
(3)运用以上得到的公式,计算:(x﹣2y+3z)(x+2y﹣3z)
查看答案和解析>>
科目:初中数学 来源: 题型:
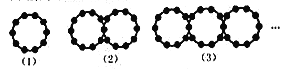
【题目】观察如图所示的一组图形,其中图形①中共有2颗星,图形②中共有6颗星,图形③中共有11颗星,图形④中共有17颗星,…,按此规律,图形⑧中星星的颗数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填写下表
序号 |
| 1 | 2 | … |
① |
| 5 |
| … |
② |
| 2 |
| … |
③ |
|
| 4 | … |
随着![]() 值的逐渐变大,回答下列问题
值的逐渐变大,回答下列问题
(1)当![]() 时,这三个代数式中 的值最小;
时,这三个代数式中 的值最小;
(2)你预计代数式的值最先超过1000的是代数式 ,此时![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上![]() 点表示数
点表示数![]() ,
,![]() 点表示数
点表示数![]() ,
,![]() 表示
表示![]() 点和
点和![]() 点之间的距离,且
点之间的距离,且![]() 、
、![]() 满足
满足![]() 数轴上有一动点
数轴上有一动点![]() ,从
,从![]() 点出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为
点出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为![]() 秒
秒![]() ,
,
![]()
(1)点![]() 表示的数为 ,点
表示的数为 ,点![]() 表示的数为 .
表示的数为 .
(2)点![]() 表示的数 (用含
表示的数 (用含![]() 的代数式表示);
的代数式表示);
(3)当点![]() 运动 秒时,点
运动 秒时,点![]() 和点
和点![]() 之间距离为4;
之间距离为4;
(4)若数轴上另有一动点![]() ,同时从
,同时从![]() 点出发,以每秒1个单位长度的速度沿数轴向左匀速运动,当点
点出发,以每秒1个单位长度的速度沿数轴向左匀速运动,当点![]() 和点
和点![]() 之间距离为6时,求时间
之间距离为6时,求时间![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是工人师傅用同一种材料制成的金属框架,已知∠B=∠E,AB=DE,BF=EC,其中△ABC的周长为24cm,CF=3cm,则制成整个金属框架所需这种材料的总长度为 ________cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了庆祝元旦,某商场在门前的空地上用花盆排列出了如图所示的图案,第1个图案中有10个花盆,第2个图案中有19个花盆,…,按此规律排列下去.
(1)第3个图案中有______个花盆,第4个图案中有______个花盆;
(2)根据上述规律,求出第![]() 个图案中花盆的个数(用含
个图案中花盆的个数(用含![]() 的代数式表示);
的代数式表示);
(3)是否存在恰好由2026个花盆排列出的具有上述规律的图案?若存在,说明它是第几个图案?若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
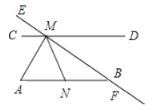
【题目】如图,∠CME+∠ABF=180°,MA平分∠CMN.若∠MNA=62°,求∠A的度数.根据提示将解题过程补充完整.
解:因为∠ABM+∠ABF=180°,
又因为∠CME+∠ABF=180°(已知),
所以∠ABM=∠CME
所以AB∥CD,理由:( )
所以∠CMN+( )=180°,
理由:(__________________________)
因为∠MNA=62°,
所以∠CMN=( )
因为MA平分∠CMN,
所以∠AMC=![]() ∠CMN =( ).(角平分线的定义)
∠CMN =( ).(角平分线的定义)
因为AB∥CD,
所以∠A=∠AMC=( )理由:(__________________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
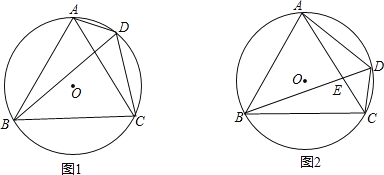
【题目】已知:等边三角形△ABC内接于⊙O,点D在![]() 上,连接AD、CD、BD,
上,连接AD、CD、BD,
(1)如图1,求证:∠ADB=∠BDC=60°;
(2)如图2,若BD=3CD,求证:AE=2CE;
(3)在(2)的条件下,连接OE,若BE=14,求线段OE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com