
【题目】如图,菱形ABCD的较短对角线BD为4,∠ADB=60°,E、F分别在AD,CD上,且∠EBF=60°.
(1)求证:△ABE≌△DBF;
(2)判断△BEF的形状,并说明理由.

【答案】(1)证明见解析;(2)结论:△BEF是等边三角形.理由见解析.
【解析】
(1)首先证明△ABD,△BDC都是等边三角形,再证明∠ABE=∠DBF,即可解决问题;
(2)根据全等三角形的性质可知BE=BF,结合∠EBF=60°即可证明;
(1)证明:∵四边形ABCD是菱形,
∴AD=AB,
∵∠ADB=60°,
∴△ADB是等边三角形,△BDC是等边三角形,
∴AB=BD,∠ABD=∠A=∠BDC=60°,
∵∠ABD=∠EBF=60°,
∴∠ABE=∠DBF,
在△ABE和△DBF中,
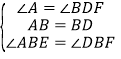 ,
,
∴△ABE≌△DBF.
(2)结论:△BEF是等边三角形.
理由:∵△ABE≌△DBF,
∴BE=BF,∵∠EBF=60°,
∴△EBF是等边三角形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某文化用品商店用1 000元购进一批“晨光”套尺,很快销售一空;商店又用1 500元购进第二批该款套尺,购进时单价是第一批的![]() 倍,所购数量比第一批多100套.
倍,所购数量比第一批多100套.
(1)求第一批套尺购进时单价是多少?
(2)若商店以每套4元的价格将这两批套尺全部售出,可以盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的边OA与x轴重合,B的坐标为(﹣1,2),将矩形OABC绕平面内一点P顺时针旋转90°,使A、C两点恰好落在反比例函数![]() 的图象上,则旋转中心P点的坐标是( )
的图象上,则旋转中心P点的坐标是( )

A. (![]() ,﹣
,﹣![]() ) B. (
) B. (![]() ,﹣
,﹣![]() ) C. (
) C. (![]() ,﹣
,﹣![]() ) D. (
) D. (![]() ,﹣
,﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,分别在AB的右侧、AC的左侧作等边△ABE和等边△ACD,BE与CD相交于点F,连接BD,若BD=BF,则∠BDF为__________度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段BC=8,射线CG⊥BC,A为射线CG上一点,已知FA⊥AB且FA=AB,AE平分∠FAB,且E点满足∠EBA=∠ABC.

(1)求证:△ABE≌△AFE.
(2)证明:FD⊥BC.
(3)求△BED的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是![]() 的中线,E是AD上一点,连接BE并延长交AC于点F,若EF=AF, BE=7.5, CF=6,则EF=( ).
的中线,E是AD上一点,连接BE并延长交AC于点F,若EF=AF, BE=7.5, CF=6,则EF=( ).
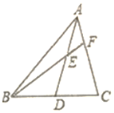
A.2.5B.2C.1.5D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知k为任意实数,随着k的变化,抛物线y=x2﹣2(k﹣1)x+k2﹣3的顶点随之运动,则顶点运动时经过的路径与两条坐标轴围成图形的面积是( )
A. 1 B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=3,AD=6,点E是边AD上的一个动点,把△BAE沿BE折叠,若点A的对应点A′恰落在矩形ABCD的对称轴上,则AE=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com