练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，将△ABC绕点A按顺时针方向旋转某个角度得到△APQ，使AP平行于CB，CB，AQ的延长线相交于点D．如果∠D=40°，则∠BAC的度数为（　　）

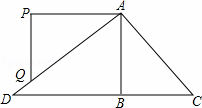
    　 A． 30° B． 40° C． 50° D． 60°


    B

    考点： 旋转的性质． 

    分析： 如图，首先由旋转变换的性质得到∠PAQ=∠BAC；由平行线的性质得到∠PAQ=∠D=40°，即可解决问题．

    解答： 解：如图，由旋转变换的性质得：

    ∠PAQ=∠BAC；

    ∵AP∥BD，

    ∴∠PAQ=∠D=40°，

    ∴∠BAC=40°．

    故选B．

    点评： 该题主要考查了旋转变换的性质、平行线的性质等几何知识点及其应用问题，灵活运用旋转变换的性质来分析、判断、推理或解答是解题的关键．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    若x，y互为倒数，m，n互为相反数，则=　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列计算正确的是（　　）

    A． 6a3•6a4=6a7   B．（2+a）2=4+2a+ a2   C．（3a3）2=6a6   D．（π﹣3.14）0=1

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在平行四边形ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，求证  （1）EF=CF；（2）∠DFE=3∠AEF．（8分）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列式子化简后的结果为x6的是（　　）

    　 A． x3+x3 B． x3•x3 C． （x3）3 D． x12÷x2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知平行四边形ABCD中，AB=5，BC=8，cosB=，点E是BC边上的动点，当以CE为半径的圆C与边AD不相交时，半径CE的取值范围是（　　）

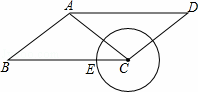
    　 A． 0＜CE≤8 B． 0＜CE≤5

    　 C． 0＜CE＜3或5＜CE≤8 D． 3＜CE≤5

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在△ABC中，AH⊥BC于点H，点P从B点开始出发向C点运动，在运动过程中，设线段AP的长为y，线段BP的长为x（如图1），而y关于x的函数图象如图2所示．Q （1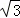，）是函数图象上的最低点．小明仔细观察图1，图2两图，作出如下结论：①AB=2；②AH=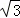；③AC=2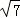；④x=2时，△ABP是等腰三角形；⑤若△ABP为钝角三角形，则0＜x＜1；其中正确的是　　（填写序号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


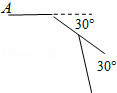
    如图，王老师在上多边形外角和这节课时，做了一个活动，让小明在操场上从A点出发前进1m，向右转30°，再前进1m，又向右转30°，…，这样一直走下去，直到他第一次回到出发点A为止，他所走的路径构成了一个多边形．小明一共走了　　m，这个多边形的内角和是　          　度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列命题中，正确的是（      ）

    A、相等的角是对顶角。            B、等腰三角形都相似。

    C、位似图形上任意一对对应点到位似中心的距离之比等于位似比。

    D、对角线互相垂直平分的四边形是正方形。

    查看答案和解析>>

    同步练习册答案