
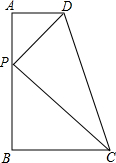
 如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=3,CD=5$\sqrt{2}$,点P在线段AB上.若△PCD是以点P为直角顶点的直角三角形,则AP=1或6.
如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=3,CD=5$\sqrt{2}$,点P在线段AB上.若△PCD是以点P为直角顶点的直角三角形,则AP=1或6. 分析 作DE⊥BC于E,则DE=AB,BE=AD=2,∠DEC=90°,得出CE,由勾股定理求出DE,得出AB,AP=x,则BP=7-x,证明△APD∽△BCP,得出对应边成比例$\frac{AP}{BC}=\frac{AD}{BP}$,解方程求出x即可即可.
解答 解:作DE⊥BC于E,如图所示: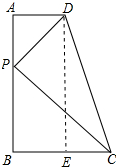 则DE=AB,BE=AD=2,∠DEC=90°,
则DE=AB,BE=AD=2,∠DEC=90°,
∴CE=BC-BE=1,
∴DE=$\sqrt{C{D}^{2}-C{E}^{2}}$=$\sqrt{50-1}$=7,
∴AB=7,
设AP=x,则BP=7-x,
∵∠CPD=90°,
∴∠APD+∠BPC=90°,
∵∠B=90°,AD∥BC,
∴∠BPC+∠BCP=90°,∠A+∠B=180°,
∴∠A=90°=∠B,∠APD=∠BCP,
∴△APD∽△BCP,
∴$\frac{AP}{BC}=\frac{AD}{BP}$,
即$\frac{x}{3}=\frac{3}{7-x}$,
解得:x=1,或x=6,
即AP=1,或AP=6;
故答案为:1或6.
点评 本题考查了直角梯形的性质、勾股定理、相似三角形的判定与性质;熟练掌握直角梯形的性质,证明三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届湖北省赤壁市九年级下学期第一次模拟(调研)考试数学试卷(解析版) 题型:选择题
如图,直线AB,CD相交于点O,射线OM平分∠AOC,ON⊥OM,若∠AOM=35°,则∠CON的度数为( )
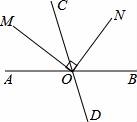
A.35° B.45° C.55° D.65°
查看答案和解析>>
科目:初中数学 来源:2017届湖北省赤壁市九年级下学期第一次模拟(调研)考试数学试卷(解析版) 题型:单选题
下列说法中,正确的是
A. “打开电视,正在播放新闻联播节目”是必然事件
B. 某种彩票中奖概率为10%是指买10张一定有一张中奖
C. 了解某种节能灯的使用寿命应采用全面检查
D. 一组数据3,5,4,6,7的中位数是5,方差是2
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2017届江西省九年级下学期第一次模拟考试数学试卷(解析版) 题型:解答题
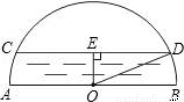
如图是一个半圆形桥洞截面示意图,圆心为O,直径AB是河底线,弦CD是水位线,CD∥AB,且CD=24 m,OE⊥CD于点E.已测得sin∠DOE=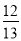 .
.
(1)求半径OD;
(2)根据需要,水面要以每小时0.5m的速度下降,则经过多长时间才能将水排干?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com