
【题目】如图,在Rt△ABC中,∠C=90°,AC=8m,BC=6m,点P由C点出发以2m/s的速度向终点A匀速移动,同时点Q由点B出发以1m/s的速度向终点C匀速移动,当一个点到达终点时另一个点也随之停止移动.
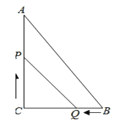
(1)经过几秒△PCQ的面积为△ACB的面积的![]() ?
?
(2)经过几秒,△PCQ与△ACB相似?
【答案】(1)2秒或4秒;(2)![]() 秒或
秒或![]() 秒
秒
【解析】
(1)分别表示出线段PC和线段CQ的长后利用S△PCQ=![]() S△ABC列出方程求解;
S△ABC列出方程求解;
(2)设运动时间为ts,△PCQ与△ACB相似,当△PCQ与△ACB相似时,则有![]() 或
或![]() ,分别代入可得到关于t的方程,可求得t的值.
,分别代入可得到关于t的方程,可求得t的值.
解:(1)设经过x秒△PCQ的面积为△ACB的面积的![]() ,
,
由题意得:PC=2xm,CQ=(6﹣x)m,
则![]() ×2x(6﹣x)=
×2x(6﹣x)=![]() ×
×![]() ×8×6,
×8×6,
解得:x=2或x=4.
故经过2秒或4秒,△PCQ的面积为△ACB的面积的![]() ;
;
(2)设运动时间为ts,△PCQ与△ACB相似.
当△PCQ与△ACB相似时,则有![]() 或
或![]() ,
,
所以![]() ,或
,或![]() ,
,
解得t=![]() ,或t=
,或t=![]() .
.
因此,经过![]() 秒或
秒或![]() 秒,△OCQ与△ACB相似;
秒,△OCQ与△ACB相似;


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】 为满足社区居民健身的需要,市政府准备采购若干套健身器材免费提供给社区,经考察,劲松公司有![]() 两种型号的健身器可供选择.
两种型号的健身器可供选择.
(1)劲松公司2015年每套![]() 型健身器的售价为
型健身器的售价为![]() 万元,经过连续两年降价,2017年每套售价为
万元,经过连续两年降价,2017年每套售价为![]() 万元,求每套
万元,求每套![]() 型健身器年平均下降率
型健身器年平均下降率![]() ;
;
(2)2017年市政府经过招标,决定年内采购并安装劲松公司![]() 两种型号的健身器材共
两种型号的健身器材共![]() 套,采购专项费总计不超过
套,采购专项费总计不超过![]() 万元,采购合同规定:每套
万元,采购合同规定:每套![]() 型健身器售价为
型健身器售价为![]() 万元,每套
万元,每套![]() 型健身器售价我
型健身器售价我![]() 万元.
万元.
①![]() 型健身器最多可购买多少套?
型健身器最多可购买多少套?
②安装完成后,若每套![]() 型和
型和![]() 型健身器一年的养护费分别是购买价的
型健身器一年的养护费分别是购买价的![]() 和
和![]() .市政府计划支出
.市政府计划支出![]() 万元进行养护.问该计划支出能否满足一年的养护需要?
万元进行养护.问该计划支出能否满足一年的养护需要?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若抛物线y=x2+ax+b与x轴两个交点间的距离为2,则称此抛物线为定弦抛物线.已知某定弦抛物线的对称轴为直线x=1,将此抛物线向左平移1个单位,再向下平移3个单位,得到的抛物线的解析式为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中,每个小正方形的边长都是1个单位长度,在Rt△OAB中,∠OAB=90°,且点B的坐标为(4,2).
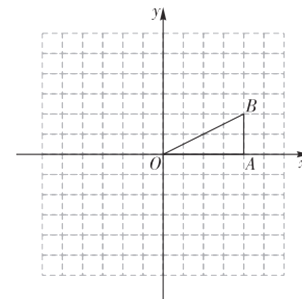
(1)画出△OAB向下平移3个单位长度后的△O1A1B1;
(2)画出△OAB绕点O逆时针旋转90°后的△OA2B2;
(3)在(2)的条件下,求点B旋转到点B2所经过的路径长(结果保留根号和π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为进一步营造扫黑除恶专项斗争的浓厚宣传氛围,推进平安校园建设,甲、乙两所学校各租用一辆大巴车组织部分师生,分别从距目的地240千米和270千米的两地同时出发,前往“研学教育”基地开展扫黑除恶教育活动,已知乙校师生所乘大巴车的平均速度是甲校师生所乘大巴车的平均速度的1.5倍,甲校师生比乙校师生晚1小时到达目的地,分别求甲、乙两所学校师生所乘大巴车的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于
轴交于![]() ,
,![]() 两点,点
两点,点![]() 在点
在点![]() 左侧.点
左侧.点![]() 的坐标为
的坐标为![]() ,
,![]() .
.
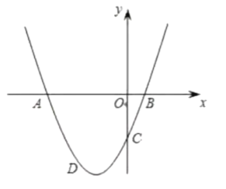
(1)求抛物线的解析式;
(2)当![]() 时,如图所示,若点
时,如图所示,若点![]() 是第三象限抛物线上方的动点,设点
是第三象限抛物线上方的动点,设点![]() 的横坐标为
的横坐标为![]() ,三角形
,三角形![]() 的面积为
的面积为![]() ,求出
,求出![]() 与
与![]() 的函数关系式,并直接写出自变量
的函数关系式,并直接写出自变量![]() 的取值范围;请问当
的取值范围;请问当![]() 为何值时,
为何值时,![]() 有最大值?最大值是多少.
有最大值?最大值是多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角三角形ABC中,ACB=90°,AC=BC=10,将△ABC绕点B沿顺时针方向旋转90°得到△A1BC1.
(1)线段A1C1的长度是 ,∠CBA1的度数是 .
(2)连结CC1,求证:四边形CBA1C1是平行四边形.
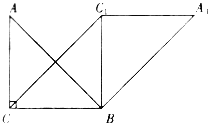
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线![]() (k为常数).
(k为常数).
(1)若抛物线经过点(1,k2),求k的值;
(2)若抛物线经过点(2k,y1)和点(2,y2),且y1>y2,求k的取值范围;
(3)若将抛物线向右平移1个单位长度得到新抛物线,当1≤x≤2时,新抛物线对应的函数有最小值![]() ,求k的值.
,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,F是⊙O上一点,连接FO、FB.C为![]() 中点,过点C作CD⊥AB,垂足为D,CD交FB于点E,CG∥FB,交AB的延长线于点G.
中点,过点C作CD⊥AB,垂足为D,CD交FB于点E,CG∥FB,交AB的延长线于点G.
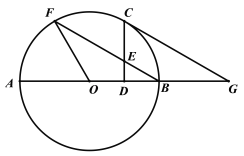
(1)求证:CG是⊙O的切线;
(2)若![]() BOF=120°,且CE=4,求⊙O的半径.
BOF=120°,且CE=4,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com