
如图,在矩形ABCD中,AB=4,AD=6,M,N分别是AB,CD的中点,P是AD上的点,且∠PNB=3∠CBN.
(1)求证:∠PNM=2∠CBN;
(2)求线段AP的长.
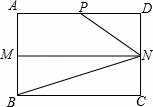
(1)由MN∥BC,易得∠CBN=∠MNB,由已知∠PNB=3∠CBN,根据角的和差不难得出结论;
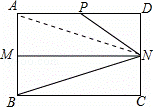
(2)连接AN,根据矩形的轴对称性,可知∠PAN=∠CBN,由(1)知∠PNM=2∠CBN=2∠PAN,由AD∥MN,可知∠PAN=∠ANM,所以∠PAN=∠PNA,根据等角对等边得到AP=PN,再用勾股定理列方程求出AP.
解答: 解:(1)∵四边形ABCD是矩形,M,N分别是AB,CD的中点,
∴MN∥BC,
∴∠CBN=∠MNB,
∵∠PNB=3∠CBN,
∴∠PNM=2∠CBN;
(2)连接AN,
根据矩形的轴对称性,可知∠PAN=∠CBN,
∵MN∥AD,
∴∠PAN=∠ANM,
由(1)知∠PNM=2∠CBN,
∴∠PAN=∠PNA,
∴AP=PN,
∵AB=CD=4,M,N分别为AB,CD的中点,
∴DN=2,
设AP=x,则PD=6﹣x,
在Rt△PDN中
PD2+DN2=PN2,
∴(6﹣x)2+22=x2,
解得:x=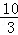
所以AP=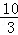 .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
下列各数表示正确的是( )
|
| A. | 57000000=57×106 |
|
| B. | 0.0158(用四舍五入法精确到0.001)=0.015 |
|
| C. | 1.804(用四舍五入法精确到十分位)=1.8 |
|
| D. | 0.0000257=2.57×10﹣4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
为有效开展阳光体育活动,云洱中学利用课外活动时间进行班级篮球比赛,每场比赛都要决出胜负,每队胜一场得2分,负一场得1分.已知九年级一班在8场比赛中得到13分,问九年级一班胜、负场数分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
下列不等式变形正确的是( )
A. 由a>b得ac >bc
>bc B. 由a>b得
B. 由a>b得 ﹣2a>﹣2b
﹣2a>﹣2b
C. 由a>b得﹣a<﹣b D. 由a>b得a﹣2<b﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
某中学女子足球队15名队员的年龄情况如下表:
年龄(岁) 13 14 15 16
队员(人) 2 3 6 4
这支球队队员的年龄的众数和中位数分别是( )
A. 14,15 B. 14,14.5 C. 15,15 D. 15,14
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com