
【题目】如图,正方形![]() 的顶点
的顶点![]() 、
、![]() 在圆
在圆![]() 上,若
上,若![]()
![]() ,圆
,圆![]() 的半径为2
的半径为2![]() ,则阴影部分的面积是__________
,则阴影部分的面积是__________![]() .(结果保留根号和
.(结果保留根号和![]() )
)

【答案】![]()
【解析】
设AD和BC分别与圆交于点E和F,连接AF、OE,过点O作OG⊥AE,根据90°的圆周角对应的弦是直径,可得AF为圆![]() 的直径,从而求出AF,然后根据锐角三角函数和勾股定理,即可求出∠AFB和BF,然后根据平行线的性质、锐角三角函数和圆周角定理,即可求出OG、AG和∠EOF,最后利用S阴影=S梯形AFCD-S△AOE-S扇形EOF计算即可.
的直径,从而求出AF,然后根据锐角三角函数和勾股定理,即可求出∠AFB和BF,然后根据平行线的性质、锐角三角函数和圆周角定理,即可求出OG、AG和∠EOF,最后利用S阴影=S梯形AFCD-S△AOE-S扇形EOF计算即可.
解:设AD和BC分别与圆交于点E和F,连接AF、OE,过点O作OG⊥AE

∵四边形ABCD是正方形
∴∠ABF=90°,AD∥BC,BC=CD=AD=![]() cm
cm
∴AF为圆![]() 的直径
的直径
∵![]()
![]() ,圆
,圆![]() 的半径为2
的半径为2![]() ,
,
∴AF=4cm
在Rt△ABF中sin∠AFB=![]() ,BF=
,BF=![]()
∴∠AFB=60°,FC=BC-BF=![]()
∴∠EAF=∠AFB=60°
∴∠EOF=2∠EAF=120°
在Rt△AOG中,OG=sin∠EAF·AO=![]() ,AG= cos∠EAF·AO=1cm
,AG= cos∠EAF·AO=1cm
根据垂径定理,AE=2AG=2cm
∴S阴影=S梯形AFCD-S△AOE-S扇形EOF
=![]()
=![]()
=![]()
故答案为:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
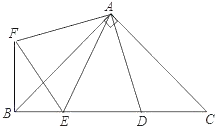
【题目】如图,在Rt△ABC中,AB=AC,D、E是斜边BC上的两点,∠EAD=45°,将△ADC绕点A顺时针旋转90°,得到△AFB,连接EF.
(1)求证:EF=ED;
(2)若AB=2![]() ,CD=1,求FE的长.
,CD=1,求FE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
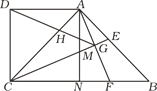
【题目】如图,在四边形ABCD中,AD∥BC,∠BCD=90°,∠ABC=45°,AD=CD,CE平分∠ACB交AB于点E,在BC上截取BF=AE,连接AF交CE于点G,连接DG交AC于点H,过点A作AN⊥BC,垂足为N,AN交CE于点M.则下列结论;①CM=AF;②CE⊥AF;③△ABF∽△DAH;④GD平分∠AGC,其中正确的序号是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
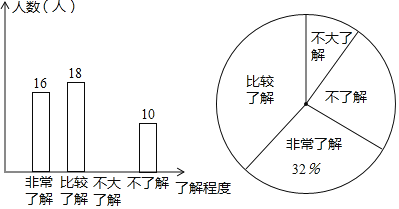
【题目】某校为了解学生对“第二十届中国哈尔滨冰雪大世界”主题景观的了解情况,在全体学生中随机抽取了部分学生进行调查,并把调查结果绘制成如图的不完整的两幅统计图:
(1)本次调查共抽取了多少名学生;
(2)通过计算补全条形图;
(3)若该学校共有![]() 名学生,请你估计该学校选择“比较了解”项目的学生有多少名?
名学生,请你估计该学校选择“比较了解”项目的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)如图所示,下列结论中:
①4ac-b2<0;②3b+2c<0;③4a+c<2b;④m(am+b)+b<a(m≠-1).
其中正确的结论有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
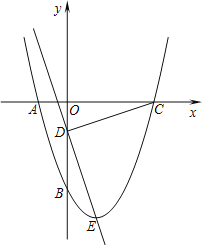
【题目】如图所示,抛物线y=x2+bx+c经过A、B两点,A、B两点的坐标分别为(﹣1,0)、(0,﹣3).
(1)求抛物线的函数解析式;
(2)点E为抛物线的顶点,点C为抛物线与x轴的另一交点,点D为y轴上一点,且DC=DE,求出点D的坐标;
(3)在第二问的条件下,在直线DE上存在点P,使得以C、D、P为顶点的三角形与△DOC相似,请你直接写出所有满足条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
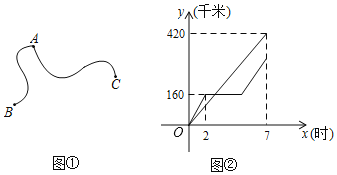
【题目】如图①,甲、乙两车同时从A地出发,分别匀速前往B地与C地,甲车到达B地休息一段时间后原速返回,乙车到达C地后立即返回.两车恰好同时返回A地.图②是两车各自行驶的路程y(千米)与出发时间x(时)之间的函数图象.根据图象解答下列问题:
(1)甲车到达B地休息了 时;
(2)求甲车返回A地途中y与x之间的函数关系式;
(3)当x为何值时,两车与A地的路程恰好相同.(不考虑两车同在A地的情况)
查看答案和解析>>
科目:初中数学 来源: 题型:
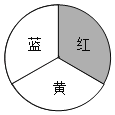
【题目】某商场开业,为了活跃气氛,用红、黄、蓝三色均分的转盘设计了两种抽奖方案,凡来商场消费的顾客都可以选择一种抽奖方案进行抽奖.
方案一:转动转盘一次,指针落在红色区域可领取一份奖品;
方案二:转动转盘两次,指针落在不同颜色区域可领取一份奖品,你会选择哪个方案?请用相关的数学知识说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com