
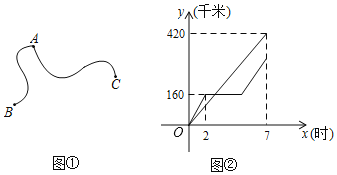
【题目】如图①,甲、乙两车同时从A地出发,分别匀速前往B地与C地,甲车到达B地休息一段时间后原速返回,乙车到达C地后立即返回.两车恰好同时返回A地.图②是两车各自行驶的路程y(千米)与出发时间x(时)之间的函数图象.根据图象解答下列问题:
(1)甲车到达B地休息了 时;
(2)求甲车返回A地途中y与x之间的函数关系式;
(3)当x为何值时,两车与A地的路程恰好相同.(不考虑两车同在A地的情况)
【答案】(1)3小时;(2)y=80x﹣240;(3)当x为![]() 或
或![]() 时,两车与A 地的距离恰好相同
时,两车与A 地的距离恰好相同
【解析】
(1)根据题意和图象中的数据可以求得甲车到达B地休息了多长时间;
(2)根据函数图象中的数据利用待定系数法可以求得甲车返回A地途中y与x之间的函数关系式;
(3)根据函数图象中的数据可以求得甲、乙的速度,根据甲、乙两车所在的位置分类讨论,分别列出对应的方程,从而可以解答本题.
解:(1)由题意可得,
甲车到达B地休息了:7﹣2﹣2=3(小时),
故答案为:3小时;
(2)设 甲车返回A地途中y与x之间的函数关系式是y=kx+b,
将(2+3,160)和(7,320)代入,得
![]() ,
,
得![]() ,
,
即甲车返回A地途中y与x之间的函数关系式是y=80x﹣240;
(3)甲车的速度为160÷2=80km/h,
乙车的速度为:420÷7=60km/h,
A、C两地的距离为420÷2=210
∴甲车到达点C需要210÷60=![]() 小时
小时
当0<x≤2时,
∵甲车速度>乙车速度
∴此时不存在x,使两车与A地的路程恰好相同;
当2<x≤![]() 时,此时甲车休息,距A地160千米,而乙车还未到C地
时,此时甲车休息,距A地160千米,而乙车还未到C地
∴60x=160,得x=![]() ;
;
当![]() <x≤5时,此时甲车休息,距A地160千米,而乙车从C地返回
<x≤5时,此时甲车休息,距A地160千米,而乙车从C地返回
∴420-60x=160,
得x=![]() ;
;
当5<x<7时,
根据甲、乙两车同时返回到A地,而题中要求不考虑两车同在A地的情况
此时不存在x,使两车与A地的路程恰好相同.
综上所述:当x为![]() 或
或![]() 时,两车与A 地的距离恰好相同.
时,两车与A 地的距离恰好相同.


科目:初中数学 来源: 题型:
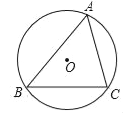
【题目】如图,△ABC内接于⊙O.
(1)作∠B的平分线与⊙O交于点D(用尺规作图,不用写作法,但要保留作图痕迹);
(2)在(1)中,连接AD,若∠BAC=60°,∠C=66°,求∠DAC的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中有三点![]() ,
,![]() ,
,![]() ,其中有两点同时在反比例函数
,其中有两点同时在反比例函数![]() 的图象上.将这两点分别记为
的图象上.将这两点分别记为![]() ,另一点记为
,另一点记为![]() .
.
(1)求出![]() 的值;
的值;
(2)求直线![]() 对应的一次函数的表达式.
对应的一次函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() ,直线
,直线![]() 与抛物线、
与抛物线、![]() 轴分别相交于
轴分别相交于![]() 、
、![]() .
.

(1)![]() 时,
时,![]() 点的坐标为________;
点的坐标为________;
(2)当![]() 、
、![]() 两点重合时,求
两点重合时,求![]() 的值;
的值;
(3)当![]() 点达到最高时,求抛物线解析式;
点达到最高时,求抛物线解析式;
(4)在抛物线![]() 与
与![]() 轴所围成的封闭图形的边界上,我们把横坐标是整数的点称为“可点”,直接写出
轴所围成的封闭图形的边界上,我们把横坐标是整数的点称为“可点”,直接写出![]() 时“可点”的个数为____.
时“可点”的个数为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中.点E,F分别在BC,CD上,△AEF是等边三角形.连接AC交EF于点G.过点G作GH⊥CE于点H.若![]() ,则
,则![]() =( )
=( )

A. 6 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
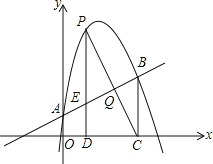
【题目】如图,抛物线y=ax2+bx+1经过点(2,6),且与直线y=![]() x+1相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).
x+1相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).
(1)求抛物线的解析式;
(2)若P是直线AB上方该抛物线上的一个动点,过点P作PD⊥x轴于点D,交AB于点E,求线段PE的最大值;
(3)在(2)的条件,设PC与AB相交于点Q,当线段PC与BE相互平分时,请求出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某学校学生的个性特长发展情况,学校决定围绕“音乐、体育、美术、书法、其它活动项目中,你参加哪一项活动(每人只限一项)的问题”,在全校范围内随机抽取部分学生进行问卷调查,并将调查结果绘制成如图所示的条形统计图,请根据图中提供的信息解答下列问题:

(1)在这次调查中一共抽查了多少名学生?
(2)求参加“音乐”活动项目的人数占抽查总人数的百分比.
(3)若全校有2400名学生,请估计该校参加“美术”活动项目的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比探究:
(1)如图1,等边△ABC内有一点P,若AP=8,BP=15,CP=17,求∠APB的大小;(提示:将△ABP绕顶点A旋转到△ACP′处)
(2)如图2,在△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点,且∠EAF=45°.求证:EF2=BE2+FC2;
(3)如图3,在△ABC中,∠C=90°,∠ABC=30°,点O为△ABC内一点,连接AO、BO、CO,且∠AOC=∠COB=∠BOA=120°,若AC=1,求OA+OB+OC的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com