
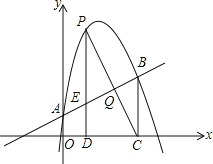
【题目】如图,抛物线y=ax2+bx+1经过点(2,6),且与直线y=![]() x+1相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).
x+1相交于A,B两点,点A在y轴上,过点B作BC⊥x轴,垂足为点C(4,0).
(1)求抛物线的解析式;
(2)若P是直线AB上方该抛物线上的一个动点,过点P作PD⊥x轴于点D,交AB于点E,求线段PE的最大值;
(3)在(2)的条件,设PC与AB相交于点Q,当线段PC与BE相互平分时,请求出点Q的坐标.
【答案】(1)y=-x2+![]() x+1;(2)当x=2时,PE的最大值为4;(3)点Q的坐标为(
x+1;(2)当x=2时,PE的最大值为4;(3)点Q的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
(1)利用直线解析式可求得B点坐标,再利用待定系数法可求得抛物线解析式;
(2)设出P点坐标,则可表示出E点坐标,则可表示出PE的长,利用二次函数的性质可求得PE的最大值;
(3)由条件可知四边形BCEP为平行四边形,可得BC=PE,则可求得P点坐标,利用中点坐标可求得Q点坐标.
(1)∵BC⊥x轴,垂足为点C(4,0),且点B在直线y=![]() x+1上,
x+1上,
∴点B的坐标为(4,3),
∴抛物线y=ax2+bx+1经过点(2,6)和点B(4,3),
∴![]() ,解得
,解得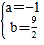 ,
,
∴抛物线的解析式为y=-x2+![]() x+1;
x+1;
(2)设动点P的坐标为(x,-x2+![]() x+1),则点E的坐标为:(x,
x+1),则点E的坐标为:(x,![]() x+1),
x+1),
∵PD⊥x轴于点D,且点P在x轴上,
∴PE=PD-ED=-x2+![]() x+1-(
x+1-(![]() x+1)=-x2+4x=-(x-2)2+4,
x+1)=-x2+4x=-(x-2)2+4,
∴当x=2时,PE的最大值为4;
(3)∵PC与BE互相平分,
∴四边形BCEP为平行四边形,
∴PE=BC,
∴-x2+4x=3即x2-4x+3=0,解得x1=1,x2=3,
∵点Q分别是PC,BE的中点,且点Q在直线y=![]() x+1
x+1
∴①当x=1时,点Q的横坐标为![]() ,点Q的坐标为(
,点Q的坐标为(![]() ,
,![]() ),
),
②当x=3时,点Q的横坐标为![]() ,点Q的坐标为(
,点Q的坐标为(![]() ,
,![]() ),
),
综上可知点Q的坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】诗词是中华民族灿烂文化中的瑰宝,王老师连续三个月在班上开展针对全班同学的古诗词默写的测试活动.如图,王老师将三次默写的成绩(满分10分)做了统计,并绘制了折线统计图.由图可知,以下结论错误的是( )
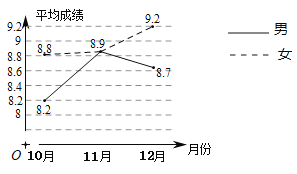
A.男、女生11月份的平均成绩相同
B.10月到12月,女生的平均成绩一直在进步
C.10月到11月,女生的平均成绩的增长率约为8.5%
D.11月到12月女生的平均成绩比10月到11月的增长快
查看答案和解析>>
科目:初中数学 来源: 题型:
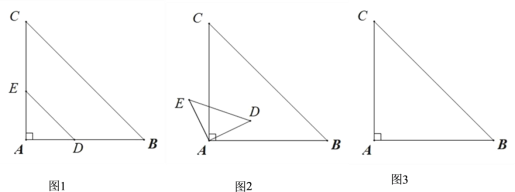
【题目】如图 1,在等腰直角△ABC 中,∠A =90°,AB=AC=3,在边 AB 上取一点 D(点 D 不与点 A,B 重合),在边 AC 上取一点 E,使 AE=AD,连接 DE. 把△ADE 绕点 A 逆时针方向旋转α(0°<α<360°),如图 2.
(1)请你在图 2 中,连接 CE 和 BD,判断线段 CE 和 BD 的数量关系,并说明理由;
(2)请你在图 3 中,画出当α =45°时的图形,连接 CE 和 BE,求出此时△CBE 的面积;
(3)若 AD=1,点 M 是 CD 的中点,在△ADE 绕点 A 逆时针方向旋转的过程中,线段AM 的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
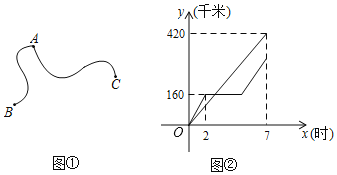
【题目】如图①,甲、乙两车同时从A地出发,分别匀速前往B地与C地,甲车到达B地休息一段时间后原速返回,乙车到达C地后立即返回.两车恰好同时返回A地.图②是两车各自行驶的路程y(千米)与出发时间x(时)之间的函数图象.根据图象解答下列问题:
(1)甲车到达B地休息了 时;
(2)求甲车返回A地途中y与x之间的函数关系式;
(3)当x为何值时,两车与A地的路程恰好相同.(不考虑两车同在A地的情况)
查看答案和解析>>
科目:初中数学 来源: 题型:
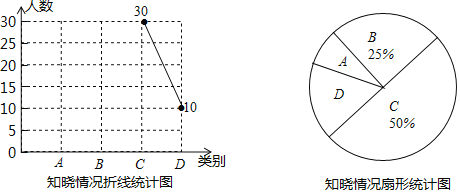
【题目】2018年5月13日,大国重器﹣﹣中国第一艘国产航母正式海试,某校团支部为了了解同学们对此事的知晓情况,随机抽取了部分同学进行调查,并根据收集到的信息绘制了如下两幅不完整的统计图,图中A表示“知道得很详细”,B表示“知道个大概”,C表示“听说了”,D表示“完全不知道”,请根据途中提供的信息完成下列问题:
(1)扇形统计图中A对应的圆心角是 度,并补全折线统计图.
(2)被抽取的同学中有4位同学都是班级的信息员,其中有一位信息员属于D类,校团支部从这4位信息员中随机选出两位作为校广播站某访谈节目的嘉宾,请用列表法或画树状图法,求出属于D类的信息员被选为的嘉宾的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装商城每月付给销售人员的工资有两种方案,已知计件工资与销售件数成正比例.有甲、乙两种品牌服装销售人员,如果销售量为![]() 件,销售甲品牌服装的工资是
件,销售甲品牌服装的工资是![]() (元),销售乙品牌服装的工资是
(元),销售乙品牌服装的工资是![]() (元),销售件数与工资之间的关系如图所示,已知销售甲品牌服装的每月底薪是800元,每销售一件甲品牌服装每件所得的提成比乙高2元,不管销售那种品牌服装,销售量超过80件(不含80件),
(元),销售件数与工资之间的关系如图所示,已知销售甲品牌服装的每月底薪是800元,每销售一件甲品牌服装每件所得的提成比乙高2元,不管销售那种品牌服装,销售量超过80件(不含80件),
则每件多提成6元.下表是半年内甲乙两产品的销售量:
时间 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 |
甲品牌服装销量 | 90 | 120 | 130 | 80 | 100 | 110 |
乙品牌服装销量 | 70 | 60 | 90 | 80 | 110 | 100 |
(1)现从半年内随机抽取1个月,求这一月乙品牌服装销售量超过80件(不含80)的概率;
(2)根据图中信息,求销售乙品牌服装的底薪是多少元?
(3)小明拟销售甲、乙两种品牌服装,如果仅从工资收人的角度考虑,请利用所学的统计知识帮他选择,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形OABC的一个顶点B的坐标是(4,2),反比例函数y=![]() (x>0)的图象经过矩形的对称中点E,且与边BC交于点D,若过点D的直线y=mx+n将矩形OABC的面积分成3:5的两部分,则此直线的解析式为_____.
(x>0)的图象经过矩形的对称中点E,且与边BC交于点D,若过点D的直线y=mx+n将矩形OABC的面积分成3:5的两部分,则此直线的解析式为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解今年灌阳县3000名七年级学生“地理知识大赛”的笔试情况,随机抽取了部分参赛同学的成绩,整理并制作如图所示的图表(部分未完成).请你根据表中提供的信息,解答下列问题:
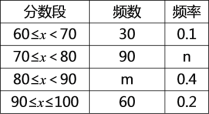
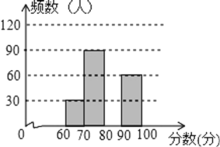
(1)此次调查的样本容量为______;m=______;n=______;
(2)补全频数分布直方图;
(3)如果比赛成绩80分以上为优秀,那么你估计灌阳县七年级学生笔试成绩的优秀人数大约是______名.
查看答案和解析>>
科目:初中数学 来源: 题型:
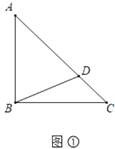
【题目】(问题提出)
(1)如图①,在等腰![]() 中,斜边
中,斜边![]() ,点
,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,则
,则![]() 的最小值为 .
的最小值为 .
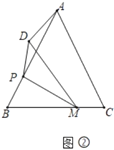
(问题探究)
(2)如图2,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 上一点,且
上一点,且![]() ,点
,点![]() 是边
是边![]() 上一动点,连接
上一动点,连接![]() ,将
,将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,点
,点![]() 与点
与点![]() 对应,连接
对应,连接![]() ,求
,求![]() 的最小值.
的最小值.
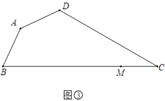
(问题解决)
(3)如图③,四边形![]() 是规划中的休闲广场示意图,其中
是规划中的休闲广场示意图,其中![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 上一点,
上一点,![]() .现计划在四边形
.现计划在四边形![]() 内选取一点
内选取一点![]() ,把
,把![]() 建成商业活动区,其余部分建成景观绿化区.为方便进入商业区,需修建小路
建成商业活动区,其余部分建成景观绿化区.为方便进入商业区,需修建小路![]() 、
、![]() ,从实用和美观的角度,要求满足
,从实用和美观的角度,要求满足![]() ,且景观绿化区面积足够大,即
,且景观绿化区面积足够大,即![]() 区域面积尽可能小.则在四边形
区域面积尽可能小.则在四边形![]() 内是否存在这样的点
内是否存在这样的点![]() ?若存在,请求出
?若存在,请求出![]() 面积的最小值;若不存在,请说明理由.
面积的最小值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com