
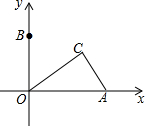
 如图,在平面直角坐标系中,点A的坐标为(4,0),点B为y轴正半轴上一点,点C是第一象限内一动点,且AC的长始终为2,则∠BOC度数的取值范围为60°≤∠BOC<90°.
如图,在平面直角坐标系中,点A的坐标为(4,0),点B为y轴正半轴上一点,点C是第一象限内一动点,且AC的长始终为2,则∠BOC度数的取值范围为60°≤∠BOC<90°. 分析 C在以A为圆心,以2为半径的圆周上,只有当OC与圆A相切(即到C点)时,∠BOC最小,根据勾股定理求出此时的OC,求出∠BOC=∠CAO,根据解直角三角形求出此时的值,根据tan∠BOC的增减性,即可求出答案.
解答 解:C在以A为圆心,以2为半径作圆,只有当OC与圆A相切(即到C点)时,∠BOC最小,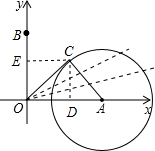
∵AC=2,OA=4,
∴OC=$\sqrt{{OA}^{2}{-AC}^{2}}$=2$\sqrt{3}$,
∵∠BOA=∠ACO=90°,
∴∠BOC+∠AOC=90°,∠CAO+∠AOC=90°,
∴∠BOC=∠OAC,
tan∠BOC=tan∠OAC=$\frac{OC}{AC}$=$\sqrt{3}$,
∴∠BOC=60°
随着C的移动,∠BOC越来越大,
∵C在第一象限,
∴C不到x轴点,
即∠BOC<90°,
∴60°≤∠BOC<90°,
故答案为:60°≤∠BOC<90°.
点评 本题考查了解直角三角形,勾股定理,切线的性质等知识点的应用,能确定∠BOC的变化范围是解此题的关键,题型比较好,但是有一定的难度.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 11×104 | B. | 0.11×107 | C. | 1.1×106 | D. | 1.1×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
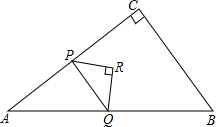 如图,在△ABC中,∠C=90°,AC=4,BC=3,点P从点A出发,以每秒4个单位长度的速度沿折线AC-CB运动,到点B停止.当点P不与△ABC的顶点重合时,过点P作其所在直角边的垂线交AB 于点Q,再以PQ为斜边作等腰直角三角形△PQR,且点R与△ABC的另一条直角边始终在PQ同侧,设△PQR与△ABC重叠部分图形的面积为S(平方单位).点P的运动时间为t(秒).
如图,在△ABC中,∠C=90°,AC=4,BC=3,点P从点A出发,以每秒4个单位长度的速度沿折线AC-CB运动,到点B停止.当点P不与△ABC的顶点重合时,过点P作其所在直角边的垂线交AB 于点Q,再以PQ为斜边作等腰直角三角形△PQR,且点R与△ABC的另一条直角边始终在PQ同侧,设△PQR与△ABC重叠部分图形的面积为S(平方单位).点P的运动时间为t(秒).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
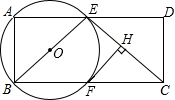 已知矩形ABCD中,AB=2,AD=5,点E是AD边上一动点,连接BE,CE,以BE为直径作⊙O,交BC于点F,过点F作FH⊥CE于点H,直线FH交⊙O于点G.
已知矩形ABCD中,AB=2,AD=5,点E是AD边上一动点,连接BE,CE,以BE为直径作⊙O,交BC于点F,过点F作FH⊥CE于点H,直线FH交⊙O于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
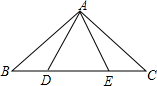 如图,点B、D、E、C在一条直线上,△ABD≌△ACE,AB和AC,AD和AE是对应边,除△ABD≌△ACE外,图中还有其他全等三角形吗?若有,请写出来,并证明你的结论.
如图,点B、D、E、C在一条直线上,△ABD≌△ACE,AB和AC,AD和AE是对应边,除△ABD≌△ACE外,图中还有其他全等三角形吗?若有,请写出来,并证明你的结论.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
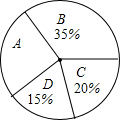 某中学九年级1班全体同学的综合素质评价“运动与健康”方面的等级统计如图所示,
某中学九年级1班全体同学的综合素质评价“运动与健康”方面的等级统计如图所示,| A. | 120° | B. | 108° | C. | 90° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{\sqrt{5}}{3}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com