
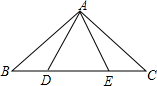
 如图,点B、D、E、C在一条直线上,△ABD≌△ACE,AB和AC,AD和AE是对应边,除△ABD≌△ACE外,图中还有其他全等三角形吗?若有,请写出来,并证明你的结论.
如图,点B、D、E、C在一条直线上,△ABD≌△ACE,AB和AC,AD和AE是对应边,除△ABD≌△ACE外,图中还有其他全等三角形吗?若有,请写出来,并证明你的结论.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
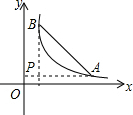 如图,A,B为反比例函数位于第一象限内图象上的点,过点A作x轴的垂线与过点B作y轴垂线交于点P,如果△ABP为等腰直角三角形且A点坐标为(5,1),则△ABP的面积为8.
如图,A,B为反比例函数位于第一象限内图象上的点,过点A作x轴的垂线与过点B作y轴垂线交于点P,如果△ABP为等腰直角三角形且A点坐标为(5,1),则△ABP的面积为8.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
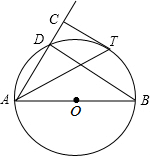 如图,AB是⊙O的直径,D为⊙O上一点,过$\widehat{BD}$上一点T作⊙O的切线TC,且TC⊥AD于点C.
如图,AB是⊙O的直径,D为⊙O上一点,过$\widehat{BD}$上一点T作⊙O的切线TC,且TC⊥AD于点C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
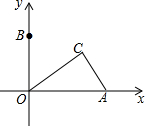 如图,在平面直角坐标系中,点A的坐标为(4,0),点B为y轴正半轴上一点,点C是第一象限内一动点,且AC的长始终为2,则∠BOC度数的取值范围为60°≤∠BOC<90°.
如图,在平面直角坐标系中,点A的坐标为(4,0),点B为y轴正半轴上一点,点C是第一象限内一动点,且AC的长始终为2,则∠BOC度数的取值范围为60°≤∠BOC<90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
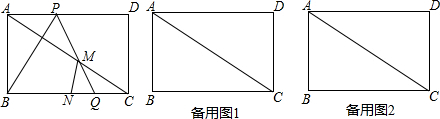
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,数轴上表示某不等式组的解集,则这个不等式组可以是( )
如图,数轴上表示某不等式组的解集,则这个不等式组可以是( )| A. | $\left\{\begin{array}{l}{x≤-2}\\{x>4}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x<-2}\\{x≥4}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x>-2}\\{x≤4}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x≥-2}\\{x<4}\end{array}\right.$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com