
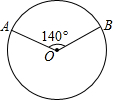
 如图,A、B是⊙O上两点,∠AOB=140°,P是⊙O上的一个动点,P不与点A、B重合,则∠APB=70°或110°.
如图,A、B是⊙O上两点,∠AOB=140°,P是⊙O上的一个动点,P不与点A、B重合,则∠APB=70°或110°. 分析 分类讨论:当点P在优弧AB上时,根据圆周角定理可得∠APB=$\frac{1}{2}$∠AOB=70°;当点P在劣弧AB上时,即点P在点P′的位置,根据圆内接四边形的性质可得∠AP′B=110°.
解答 解:如图,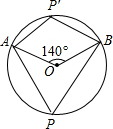
当点P在优弧AB上时,∠APB=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×140°=70°,
当点P在劣弧AB上时,即点P在点P′的位置,∠AP′B=180°-∠APB=110°,
所以∠APB为70°或110°.
故答案70°或110.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了分类讨论的思想.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
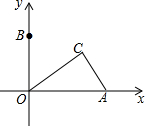 如图,在平面直角坐标系中,点A的坐标为(4,0),点B为y轴正半轴上一点,点C是第一象限内一动点,且AC的长始终为2,则∠BOC度数的取值范围为60°≤∠BOC<90°.
如图,在平面直角坐标系中,点A的坐标为(4,0),点B为y轴正半轴上一点,点C是第一象限内一动点,且AC的长始终为2,则∠BOC度数的取值范围为60°≤∠BOC<90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
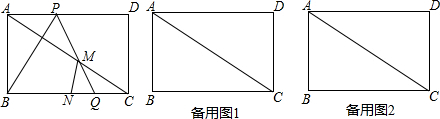
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 解不等式组:$\left\{\begin{array}{l}2x-3≤3\\ \frac{1}{2}x+1>0\end{array}\right.$,并把解集在数轴上表示出来.
解不等式组:$\left\{\begin{array}{l}2x-3≤3\\ \frac{1}{2}x+1>0\end{array}\right.$,并把解集在数轴上表示出来.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com