
| A. | 外部 | B. | 内部 | C. | 圆上 | D. | 不能确定 |
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:填空题
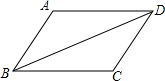 如图所示,BD是四边形ABCD的对角线,AD∥CB,请添加一个条件,使△ABD≌△CDB,这个添加的条件可以是AD=CB.(只需填一个,不添加辅助线)
如图所示,BD是四边形ABCD的对角线,AD∥CB,请添加一个条件,使△ABD≌△CDB,这个添加的条件可以是AD=CB.(只需填一个,不添加辅助线)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,PA、PB切⊙O于A、B两点,CD切⊙O于点E,交PA、PB于C、D.若⊙O的半径为2,△PCD的周长等于6,则OP=$\sqrt{13}$.
如图,PA、PB切⊙O于A、B两点,CD切⊙O于点E,交PA、PB于C、D.若⊙O的半径为2,△PCD的周长等于6,则OP=$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
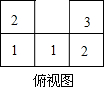 如图,是一个由小立方体搭成的几何体的俯视图(从上面看),小正方形中的数字表示在该位置的小立方体的个数,请画出它的主视图(从正面看)和左视图(从左面看).
如图,是一个由小立方体搭成的几何体的俯视图(从上面看),小正方形中的数字表示在该位置的小立方体的个数,请画出它的主视图(从正面看)和左视图(从左面看).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com