
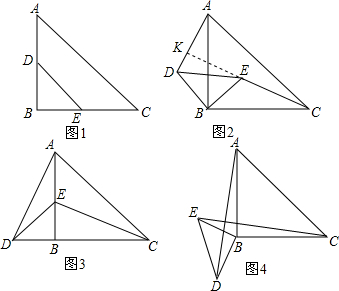
分析 (1)根据证明过程直接填空即可;
(2)先证△ADB与△CBE全等,得出CE=AD,和∠ECB=∠DAB,延长CE交AD于点F,由于∠DAB与∠ADB互余,从而∠ECB也与∠ADB互余,从而得征;
(3)方法与(2)相同;
解答 解:(1)∵∠ABC=∠EBD
∴∠ABC-∠ABE=∠EBD-∠ABE即∠EBC=∠DBA
在△EBC和△DBA中,
$\left\{\begin{array}{l}{BC=AB}\\{∠(EBC)=∠(DBA)}\\{BD=BE}\end{array}\right.$
∴△EBC≌△DBA,
∴AD=EC,∠ECB=∠DAB,
∵∠ECB+∠ACE+∠CAB=90°
∴∠DAB+∠ACE+∠CAB=90°
∴∠AKC=90°,
∴AD⊥EC.
(2)成立.如图3,
延长CE交AD于F,
在△EBC和△DBA中,
$\left\{\begin{array}{l}{BC=BA}\\{∠CBE=∠ABD}\\{BE=BD}\end{array}\right.$,
∴△EBC≌△DBA,
∴AD=EC,∠ECB=∠DAB,
∵∠DAB+∠ADB=90°,
∴∠ECB+∠ADB=90°,
∴AD⊥EC;
(3)如图4,设CE、AD交于点F,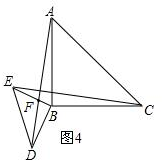
∵∠DBE=∠ABC=90°,
∴∠CBE=∠ABD,
在△EBC和△DBA中,
$\left\{\begin{array}{l}{BC=BA}\\{∠CBE=∠ABD}\\{BE=BD}\end{array}\right.$
∴△EBC≌△DBA,
∴AD=EC,∠CEB=∠ADB,
∵∠ADB+∠DFB=90°,
∴∠CEB+∠AFE=90°,
∴AD⊥EC.
点评 本题考查了等腰直角三角形的性质、全等三角形的判定与性质、三角形内角和性质、图形的旋转等知识点,难度不大,是一道基础题.事实上,本题得出了一个结论,即:两个全等的三角形如果有一个组对应相互垂直,那么另外两组对应边也相互垂直,这一结论在一些大型题目中可直接应用,会起到简化过程的作用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
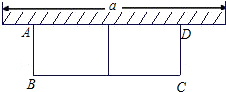 如图,有长24米的护栏,一面利用墙(墙的最大可用长度a为13m),围成中间隔有一道护栏的矩形花园,设花园的宽AB为x(m),面积为S(m2).
如图,有长24米的护栏,一面利用墙(墙的最大可用长度a为13m),围成中间隔有一道护栏的矩形花园,设花园的宽AB为x(m),面积为S(m2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com