
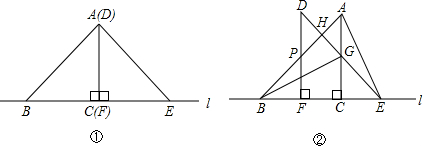
分析 (1)根据全等三角形的判定和性质解答即可;
(2)①根据等腰直角三角形的性质和全等三角形的判定和性质证明即可;
②当∠D=45°,分三种情况讨论解答即可.
解答 解:(1)在△ACB与△DFE中,
$\left\{\begin{array}{l}{AC=DF}\\{∠ACB=∠DFE}\\{BC=FE}\end{array}\right.$,
∴△ACB≌△DFE(SAS),
∴AB=DE,
∴AB=AE;
故答案为:相等;
(2)①证明:
∵△ABC和△DEF都是等腰直角三角形,
∴AC=BC,DF=EF,∠ACB=∠DFE=90°,
∴∠DEF=∠D=45°,
∴△GCE是等腰直角三角形,
同理可证△BEP是等腰直角三角形,
∴CG=CE,
∵∠ACB=∠ACE=90°,
在△BCG与△ACE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠BCG=∠ACE}\\{CG=CE}\end{array}\right.$,
∴△BCG≌△ACE(SAS).
∴BG=AE,
②存在.
∵∠D=45°,可分三种情况讨论:
(i)当∠DGB=∠D=45°时,
∵∠DGB=∠DEB+∠GBE=45°+∠GBE,
∴∠GBE=0°,即t=1,
∵平移时间0<tt<1,
∴当∠DGB=∠D=45°时,不符合题意,
(ii)同理可证,当∠DQG=∠D=45°时,不符合题意,
(iii)当∠DGB=∠DQG时,
∵∠DGB=∠DEB+∠GBE=45°+∠GBE,
∠DQG=∠BPQ+∠PBQ=45°+∠PBQ,
∴∠GBE=∠PBQ,
由已知易得∠BHE=∠ACB=90°,
∴GH=GC,
当平移时间为ts时,CF=tcm,
∴CE=CG=GH=(1-t)cm,AG=1-(1-t)=tcm,
∵BC=AC=1cm,
∴$AB=\sqrt{{1}^{2}+{1}^{2}}=\sqrt{2}$,
∵${S}_{△ABG}=\frac{1}{2}AB•GH=\frac{1}{2}AG•BC$,
∴$\sqrt{2}(1-t)=t$,解得 t=2-$\sqrt{2}$(s).
点评 此题考查几何变换问题,关键是根据全等三角形的判定和性质解答,考察的知识点比较多,难度较大,解答本题之前一定要将图形画出来,这样可以使我们的思考方向更准确一些,另外要求我们熟练掌握各个基础知识点的内容.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
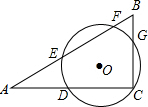 如图,△ABC中,∠ACB=90°,点O为△ABC的角平分线交点,⊙O经过点C,与△ABC的三边交于点D、E、F、G.
如图,△ABC中,∠ACB=90°,点O为△ABC的角平分线交点,⊙O经过点C,与△ABC的三边交于点D、E、F、G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
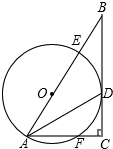 知图,在Rt△ABC中,∠C=90°,AC=12,BC=16,∠BAC的平分线交BC于D,经过A、D的⊙O交AB于E,并且点O在AB上.
知图,在Rt△ABC中,∠C=90°,AC=12,BC=16,∠BAC的平分线交BC于D,经过A、D的⊙O交AB于E,并且点O在AB上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2和$\frac{1}{2}$ | B. | $\frac{2}{5}$和-0.4 | C. | $\frac{2}{5}$和-$\frac{5}{2}$ | D. | 2和-$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
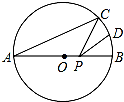 如图,AB是⊙O的直径,AB=2,点C在⊙O上,∠CAB=30°,D为弧BC的中点,P是直径AB上一动点,则PC+PD的最小值为( )
如图,AB是⊙O的直径,AB=2,点C在⊙O上,∠CAB=30°,D为弧BC的中点,P是直径AB上一动点,则PC+PD的最小值为( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com