
【题目】如图1,在平面直角坐标系中,直线AB与![]() 轴交于点A,与
轴交于点A,与![]() 轴交于点B,与直线OC:
轴交于点B,与直线OC:![]() 交于点C.
交于点C.
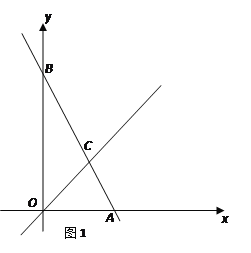

(1)若直线AB解析式为![]() ,
,
①求点C的坐标;
②求△OAC的面积.
(2)如图2,作![]() 的平分线ON,若AB⊥ON,垂足为E, OA=4,P、Q分别为线段OA、OE上的动点,连结AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.
的平分线ON,若AB⊥ON,垂足为E, OA=4,P、Q分别为线段OA、OE上的动点,连结AQ与PQ,试探索AQ+PQ是否存在最小值?若存在,求出这个最小值;若不存在,说明理由.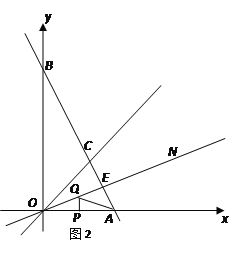
【答案】(1)①C(4,4);②12;(2)存在,3
【解析】
试题(1)①联立两个函数式,求解即可得出交点坐标,即为点C的坐标;
②欲求△OAC的面积,结合图形,可知,只要得出点A和点C的坐标即可,点C的坐标已知,利用函数关系式即可求得点A的坐标,代入面积公式即可;
(2)在OC上取点M,使OM=OP,连接MQ,易证△POQ≌△MOQ,可推出AQ+PQ=AQ+MQ;若想使得AQ+PQ存在最小值,即使得A、Q、M三点共线,又AB⊥OP,可得∠AEO=∠CEO,即证△AEO≌△CEO(ASA),又OC=OA=4,利用△OAC的面积为6,即可得出AM=3,AQ+PQ存在最小值,最小值为3.
(1)①由题意,![]()
解得![]() 所以C(4,4);
所以C(4,4);
②把![]() 代入
代入![]() 得,
得,![]() ,所以A点坐标为(6,0),
,所以A点坐标为(6,0),
所以![]() ;
;
(2)由题意,在OC上截取OM=OP,连结MQ
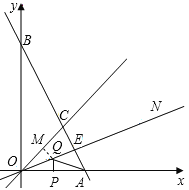
∵OQ平分∠AOC,
∴∠AOQ=∠COQ,
又OQ=OQ,
∴△POQ≌△MOQ(SAS),
∴PQ=MQ,
∴AQ+PQ=AQ+MQ,
当A、Q、M在同一直线上,且AM⊥OC时,AQ+MQ最小.
即AQ+PQ存在最小值.
∵AB⊥ON,所以∠AEO=∠CEO,
∴△AEO≌△CEO(ASA),
∴OC=OA=4,
∵△OAC的面积为12,所以AM=12÷4=3,
∴AQ+PQ存在最小值,最小值为3.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】(10分)已知∠MAN=135°,正方形ABCD绕点A旋转.
(1)当正方形ABCD旋转到∠MAN的外部(顶点A除外)时,AM,AN分别与正方形ABCD的边CB,CD的延长线交于点M,N,连接MN.
①如图1,若BM=DN,则线段MN与BM+DN之间的数量关系是 ;
②如图2,若BM≠DN,请判断①中的数量关系是否仍成立?若成立,请给予证明;若不成立,请说明理由;
(2)如图3,当正方形ABCD旋转到∠MAN的内部(顶点A除外)时,AM,AN分别与直线BD交于点M,N,探究:以线段BM,MN,DN的长度为三边长的三角形是何种三角形,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 可看成是分别以
可看成是分别以![]() 、
、![]() 、
、![]() 、
、![]() 为位似中心将正方形
为位似中心将正方形![]() 放大一倍得到的图形(正方形
放大一倍得到的图形(正方形![]() 的边长放大到原来的
的边长放大到原来的![]() 倍),由正方形
倍),由正方形![]() 到正方形
到正方形![]() ,我们称之作了一次变换,再将正方形
,我们称之作了一次变换,再将正方形![]() 作一次变换就得到正方形
作一次变换就得到正方形![]() ,…,依此下去,作了
,…,依此下去,作了![]() 次变换后得到正方形
次变换后得到正方形![]() ,若正方形
,若正方形![]() 的面积是
的面积是![]() ,那么正方形
,那么正方形![]() 的面积是多少( )
的面积是多少( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B在⊙O上,直线AC是⊙O的切线,OC⊥OB,连接AB交OC于点D.
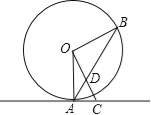
(1)AC与CD相等吗?为什么?
(2)若AC=2,AO=![]() ,求OD的长度.
,求OD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,一块Rt△ABC的绿地,量得两直角边AC=8cm,BC=6cm.现在要将这块绿地扩充成等腰△ABD,且扩充部分(△ADC)是以8cm为直角边长的直角三角形,求扩充等腰△ABD的周长.
(1)在图1中,当AB=AD=10cm时,△ABD的周长为 .
(2)在图2中,当BA=BD=10cm时,△ABD的周长为 .
(3)在图3中,当DA=DB时,求△ABD的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用![]() 个相同的小长方形与
个相同的小长方形与![]() 个小正方形镶嵌而成的正方形图案,已知该图案的面积为
个小正方形镶嵌而成的正方形图案,已知该图案的面积为![]() ,小正方形的面积为
,小正方形的面积为![]() ,若用
,若用![]() 表示小长方形的两边长(
表示小长方形的两边长(![]() ) ,请观察图案,指出以下关系式中,不正确的是( )
) ,请观察图案,指出以下关系式中,不正确的是( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润y1与投资量x成正比例关系,种植花卉的利润y2与投资量x的平方成正比例关系,并得到了表格中的数据.
投资量x(万元) | 2 |
种植树木利润y1(万元) | 4 |
种植花卉利润y2(万元) | 2 |
(1)分别求出利润y1与y2关于投资量x的函数关系式;
(2)如果这位专业户以8万元资金投入种植花卉和树木,设他投入种植花卉金额m万元,种植花卉和树木共获利利润W万元,直接写出W关于m的函数关系式,并求他至少获得多少利润?他能获取的最大利润是多少?
(3)若该专业户想获利不低于22万,在(2)的条件下,直接写出投资种植花卉的金额m的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,回答问题.
材料:为解方程x4-x2-6=0,可将方程变形为(x2)2-x2-6=0,然后设x2=y,则(x2)2=y2,原方程化为y2-y-6=0①,
解得y1=-2,y2=3.
当y1=-2时,x2=-2无意义,舍去;当y2=3时,x2=3,解得x=±![]() .
.
所以,原方程的解为x1=![]() ,x2=-
,x2=-![]() .
.
问题:
(1)在由原方程得到方程①的过程中,利用 法达到了降次的目的,体现了 的数学思想;
(2)利用本题的解题方法,解方程(x2-x)2-4(x2-x)-12=0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com