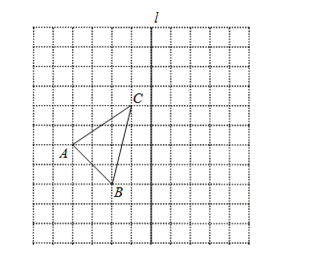
【题目】如图，在
的正方形网格中，每个小正方形的边长都为1，网格中有一个格点
（即三角形的顶点都在格点上）．
（1）在图中作出
关于直线l对称的
；（要求A与
，B与
，C与
相对应）
（2）作出绕点C顺时针方向旋转90°后得到的
；
（3）在（2）的条件下求出线段CB在旋转中所扫过的面积．（结果保留π）
科目：初中数学 来源： 题型：
【题目】如图，在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C，灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行，上午10：00在A处测得灯塔C位于轮船的北偏西30°方向，上午10：40在B处测得灯塔C位于轮船的北偏东60°方向，且与灯塔C相距12km.
(1)若轮船照此速度与航向航向，何时到达海岸线？
(2)若轮船不改变航向，该轮船能否停靠在码头？请说明理由(参考数据： 
≈1.4， 
≈1.7)．
查看答案和解析>>
科目：初中数学 来源： 题型：
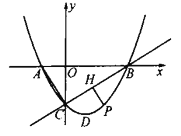
【题目】已知在平面直角坐标系中，抛物线
与
轴交于
两点（点
在点
左侧），与
轴交于点
，顶点为
．
（1）如图，直线
下方抛物线上的一个动点
（不与点
重合），过点作
于点
，当
最大时，点
为线段一点（不与点重合），当
的值最小时，求点的坐标；
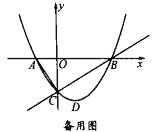
（2）将
沿直线
翻折得
，再将绕着点
顺时针旋转
得
，在旋转过程中直线
与直线相交于点
，与轴相交于点
，当
是等腰三角形时，求
的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在
中，
，将绕点
按逆时针方向旋转，得到
．
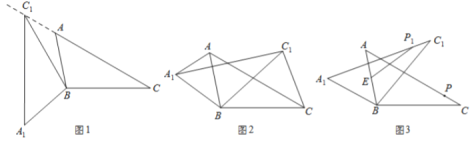
（1）如图 1，当点
在线段
的延长线上时，求
的度数；
（2）如图 2，连接
，
．若
的面积为 3，求
的面积；
（3）如图 3，点
为线段
中点，点
是线段
上的动点，在绕点按逆时针方向旋转的过程中，点的对应点是点
，求线段
长度的最大值与最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
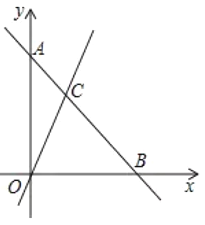
【题目】如图，在平面直角坐标系中，过点
的直线
与直线
相交于点
，动点
沿路线
运动．
（1）求直线的解析式；
（2）设
的面积
，点的横坐标为
，求出与的关系式；
（3）是否存在点，使
是直角三角形?若存在，直接写出点的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
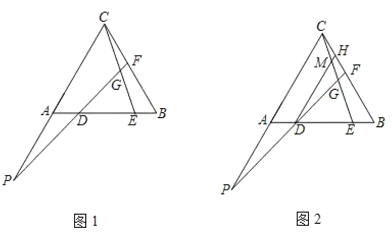
【题目】阅读下列材料：数学课上，老师出示了这样一个问题：
如图1，在等边
中，点
、
在
上，且
，直线
交
于
点，交
延长线于
点，且
，探究线段
之间的数量关系，并证明．
某学习小组的同学经过思考，交流了自己的想法：
小明：“通过观察和度量，发现
与
存在某种数量关系”；
小强：“通过观察和度量，发现图1中有一条线段与
相等”；
小伟：“通过构造三角形，证明三角形全等，进而可以得到线段之间的数量关系”．
……
老师：“保留原题条件，再过点作
交
于
与相交于点
（如图2）如果给出
的值，那么可以求出
的值”．
请回答：
（1）在图1中找出与数量关系，并证明；
（2）在图1中找出与线段相等的线段，并证明；
（3）探究线段之间的数量关系，并证明；
（4）若
，求的值（用含
的代数式表示）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小文同学统计了某栋居民楼中全体居民每周使用手机支付的次数，并绘制了直方图．根据图中信息，下列说法错误的是（ ）
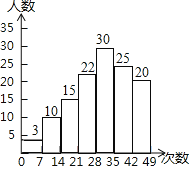
A.这栋居民楼共有居民125人
B.每周使用手机支付次数为28～35次的人数最多
C.有的人每周使用手机支付的次数在35～42次
D.每周使用手机支付不超过21次的有15人
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：关于x的方程
（1）求证：m取任何值时，方程总有实根．
（2）若二次函数
的图像关于y轴对称.
a、求二次函数
的解析式
b、已知一次函数
，证明：在实数范围内，对于同一x值，这两个函数所对应的函数值
均成立.
(3)在（2）的条件下，若二次函数
的象经过（-5,0），且在实数范围内，对于x的同一个值，这三个函数所对应的函数值
均成立，求二次函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
