
 ��ͼ���ڵ���Rt��ABC�У�AB=BC��ADƽ�֡�BAC��BC���ڵ�D����E��AD���Ͽ����˵�A��һ���㣬��AEΪ������������Rt��AEF����AE=EF���ӳ�FE��AC�ڵ�G����MΪFC�е㣬����BM��EM��BE��DM��������5�����ۣ���FA=FG���ڡ�ABD���ACD�������Ϊ1��$\sqrt{2}$����AC=��$\sqrt{2}$+1��BD���ܡ�MDC=90�㣻�ݡ�BMEΪ���������Σ�����һ��Ϊֱ�������Σ�������ȷ���У�����������
��ͼ���ڵ���Rt��ABC�У�AB=BC��ADƽ�֡�BAC��BC���ڵ�D����E��AD���Ͽ����˵�A��һ���㣬��AEΪ������������Rt��AEF����AE=EF���ӳ�FE��AC�ڵ�G����MΪFC�е㣬����BM��EM��BE��DM��������5�����ۣ���FA=FG���ڡ�ABD���ACD�������Ϊ1��$\sqrt{2}$����AC=��$\sqrt{2}$+1��BD���ܡ�MDC=90�㣻�ݡ�BMEΪ���������Σ�����һ��Ϊֱ�������Σ�������ȷ���У�����������| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
���� ����ȷ��ֻҪ֤����FAG=��FGA=67.5�㼴�ɣ�
����ȷ����DN��AC��N����ΪDAƽ�֡�BAC����DAB=��DAC������DB=DN����$\frac{{S}_{��ABD}}{{S}_{��ADC}}$=$\frac{\frac{1}{2}•AB•DB}{\frac{1}{2}•AC•DN}$=$\frac{AB}{AC}$=$\frac{1}{\sqrt{2}}$��
�۴����ɡ�ADN�ա�ADB����֪AN=AB=BC������DC=$\sqrt{2}$DN=$\sqrt{2}$BD������AC=AN+CN=BC+BD=2BD+$\sqrt{2}$BD=��2+$\sqrt{2}$��BD��
�ܴ��۲�ͼ2�����ɽ�����⣮
�ݴ�����ͼ1�У��ӳ�EM��H��ʹ��MH=EM������BH��CH�ӳ�AD��CH���ӳ�����K����֤����MFE�ա�MCH����֤����BAE�ա�BCH������֤����EBM�ǵ���ֱ�������Σ�
��� �⣺��ͼ1�У�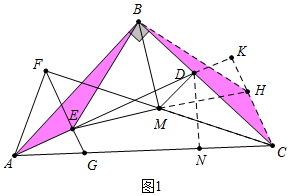
��BA=BC����ABC=90�㣬
���BAC=��BCA=45�㣬AC=$\sqrt{2}$AB��
��ADƽ�֡�BAC��
���DAB=��DAC=22.5�㣬
��EA=EF����AEF=90�㣬
���EAF=��EFA=45�㣬
��FAG=67.5�㣬��FGA=180��-��FAG-��AFE=67.5�㣬
���FAG=��FGA��
��FA=FG���ʢ���ȷ��
��DN��AC��N��
��DAƽ�֡�BAC����DAB=��DAC��
��DB=DN��
��$\frac{{S}_{��ABD}}{{S}_{��ADC}}$=$\frac{\frac{1}{2}•AB•DB}{\frac{1}{2}•AC•DN}$=$\frac{AB}{AC}$=$\frac{1}{\sqrt{2}}$���ʢ���ȷ��
�ɡ�ADN�ա�ADB����֪AN=AB=BC��
��DC=$\sqrt{2}$DN=$\sqrt{2}$BD��
��AC=AN+CN=BC+BD=2BD+$\sqrt{2}$BD=��2+$\sqrt{2}$��BD���ʢ۴���
��ͼ2�У�����M���߶�AD��ʱ����MDC=��ABD+��BAD��90�㣬�ʢܴ���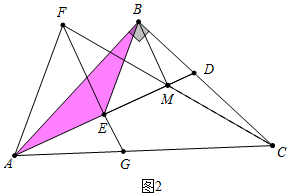
��ͼ1�У��ӳ�EM��H��ʹ��MH=EM������BH��CH�ӳ�AD��CH���ӳ�����K��
�ڡ�MFE�͡�MCH�У�
$\left\{\begin{array}{l}{MF=MC}\\{��FME=��CMH}\\{EM=MH}\end{array}\right.$��
���MFE�ա�MCH��
��CH=EF=AE����MFE=��MCH��
��EF��CK��
���FED=��K=90�㣬
�ߡ�BAE+��ADB=90�㣬��BCH+��CDK=90�㣬��ADB=��CDK��
���BAE=��BCH��
�ڡ�BAE�͡�BCH�У�
$\left\{\begin{array}{l}{BA=BC}\\{��BAE=��BCH}\\{AE=CH}\end{array}\right.$��
���BAE�ա�BCH��
��BE=BH����ABE=��CBH��
���EBH=��ABC=90�㣬��EM=MH��
��BM��EM��BM=$\frac{1}{2}$EH=EM��
���EBM�ǵ���ֱ�������Σ��ʢݴ���
��ѡA��
���� ���⿼��ȫ�������ε��ж������ʡ�����ֱ�������ε����ʡ���ƽ���ߵ����ʶ����������ε������֪ʶ������Ĺؼ���ѧ�����ӳ��ø����ߣ�����ȫ�������ν�����⣬�����п�ѡ�����е�ѹ���⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m��2 | B�� | m��2 | C�� | m��2 | D�� | m��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
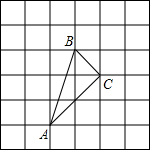 ��ͼ��С�����εı߳�Ϊ1����ABC���������㶼��С�����εĶ��㴦���жϡ�ABC����״���������ABC�������
��ͼ��С�����εı߳�Ϊ1����ABC���������㶼��С�����εĶ��㴦���жϡ�ABC����״���������ABC��������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
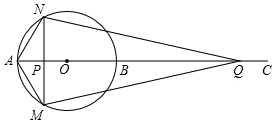 ��֪����ͼ��ABΪ��O��ֱ������CΪAB�ӳ�����һ�㣬����P�ӵ�A������AC������1cm/s���ٶ��˶���ͬʱ����Q�ӵ�C��������ͬ���ٶ���CA�����˶�������������ʱֹͣ�˶�������P��AB�Ĵ��ߣ��ֱ�O�ڵ�M�͵�N����֪��O�İ뾶Ϊ2��AC=10�����˶�ʱ��Ϊts��
��֪����ͼ��ABΪ��O��ֱ������CΪAB�ӳ�����һ�㣬����P�ӵ�A������AC������1cm/s���ٶ��˶���ͬʱ����Q�ӵ�C��������ͬ���ٶ���CA�����˶�������������ʱֹͣ�˶�������P��AB�Ĵ��ߣ��ֱ�O�ڵ�M�͵�N����֪��O�İ뾶Ϊ2��AC=10�����˶�ʱ��Ϊts���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
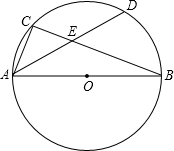 ��ͼ��ABΪ��O��ֱ����CΪ��O��һ�㣬��ADƽ�֡�BAC����BC�ڵ�E��AB=10��AD=8����AE�ij�Ϊ$\frac{7}{2}$��
��ͼ��ABΪ��O��ֱ����CΪ��O��һ�㣬��ADƽ�֡�BAC����BC�ڵ�E��AB=10��AD=8����AE�ij�Ϊ$\frac{7}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ƽ��ֱ������ϵ�У���A����ԭ��O�����ҷֱ���x�ᡢy�ύ��B��C���㣬��֪B��8��0����C��0��6�������A�İ뾶Ϊ��������
��ͼ����ƽ��ֱ������ϵ�У���A����ԭ��O�����ҷֱ���x�ᡢy�ύ��B��C���㣬��֪B��8��0����C��0��6�������A�İ뾶Ϊ��������| A�� | 5 | B�� | 6 | C�� | 8 | D�� | 10 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com