
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
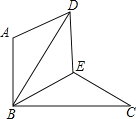
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
【答案】(1)证明见解析(2)菱形,理由见解析
【解析】
试题分析:(1)根据旋转的性质可得DB=CB,∠ABD=∠EBC,∠ABE=60°,然后根据垂直可得出∠DBE=∠CBE=30°,继而可根据SAS证明△BDE≌△BCE;
(2)根据(1)以及旋转的性质可得,△BDE≌△BCE≌△BDA,继而得出四条棱相等,证得四边形ABED为菱形.
(1)证明:∵△BAD是由△BEC在平面内绕点B旋转60°而得,
∴DB=CB,∠ABD=∠EBC,∠ABE=60°,
∵AB⊥EC,
∴∠ABC=90°,
∴∠DBE=∠CBE=30°,
在△BDE和△BCE中,
∵ ,
,
∴△BDE≌△BCE;
(2)四边形ABED为菱形;
由(1)得△BDE≌△BCE,
∵△BAD是由△BEC旋转而得,
∴△BAD≌△BEC,
∴BA=BE,AD=EC=ED,
又∵BE=CE,
∴四边形ABED为菱形.


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】若A(﹣3,y1),B(3,y3),C(2,y2)二次函数y=x2+4x﹣5的图象上的三点,则y1、y2、y3的大小关系是( )
A. y1<y2<y3 B. y2<y1<y3 C. y3<y1<y2 D. y1<y3<y2
查看答案和解析>>
科目:初中数学 来源: 题型:
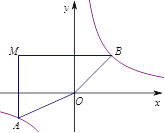
【题目】如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数y=![]() 的图象交于A、B两点,则四边形MAOB的面积为________.
的图象交于A、B两点,则四边形MAOB的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
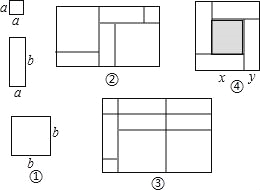
【题目】一天,王明和李玲玩纸片拼图游戏,发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式.比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.
(1)图③可以解释为等式:
(2)要拼出一个长为a+3b,宽为2a+b的长方形,需要如图所示的 块, 块, 块.
(3)如图④,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个矩形的两边长(x>y),观察图案,指出以下关系式:
①![]() ;②x+y=m;③x2﹣y2=mn;④
;②x+y=m;③x2﹣y2=mn;④![]() ,其中正确的有
,其中正确的有
A.1个 B.2个 C.3个 D.4个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】主持人问这样一道题目:“a是最小的正整数,b是最大的负整数,c是绝对值最小的有理数,请问:a,b,c三数之和是( )
A. ﹣1 B. 0 C. 1 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:P是正方形ABCD对角线AC上一点,PE⊥AB,PF⊥BC,E、F分别为垂足.
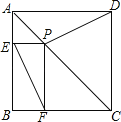
(1)求证:DP=EF.
(2)试判断DP与EF的位置关系并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com