
【题目】已知:P是正方形ABCD对角线AC上一点,PE⊥AB,PF⊥BC,E、F分别为垂足.
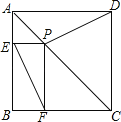
(1)求证:DP=EF.
(2)试判断DP与EF的位置关系并说明理由.
【答案】见解析
【解析】
试题分析:(1)连结PB,由正方形的性质得到BC=DC,∠BCP=∠DCP,接下来证明△CBP≌△CDP,于是得到DP=BP,然后证明四边形BFPE是矩形,由矩形的对角线相等可得到BP=EF,从而等量代换可证得问题的答案;
(2)延长DP交EF于G,延长EP交CD于H,连接PB.由(1)可知△CBP≌△CDP,依据全等三角形对应角相等可得到∠CDP=∠CBP,由四边形EPFB是矩形可证明∠CBP=∠FEP,从而得到∠HDP=∠FEP,由∠DPH+∠PDH=90°可证明∠EPG+∠PEG=90°,从而可得到问题答案.
证明:(1)如图1所示:连结PB.
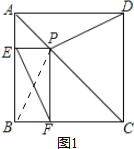
∵四边形ABCD是正方形,
∴BC=DC,∠BCP=∠DCP=45°.
∵在△CBP和△CDP中,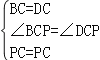 ,
,
∴△CBP≌△CDP.
∴DP=BP.
∵PE⊥AB,PF⊥BC,∠B=90°
∴四边形BFPE是矩形.
∴BP=EF.
∴DP=EF.
(2)DP⊥EF.
理由:如图2所示:延长DP交EF于G,延长EP交CD于H,连接PB.
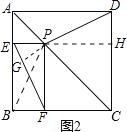
∵△CBP≌△CDP,
∴∠CDP=∠CBP.
∵四边形BFPE是矩形,
∴∠CBP=∠FEP.
∴∠CDP=∠FEP.
又∵∠EPG=∠DPH.
∴∠EGP=∠DHP.
∵PE⊥AB,AB∥DC
∴PH⊥DC.即∠DHP=90°.
∴∠EGP=∠DHP=90°
∴PG⊥EF,即DP⊥EF.


科目:初中数学 来源: 题型:
【题目】某车间有26名工人,每人每天可以生产800个螺钉或1000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套.设安排x名工人生产螺钉,则下面所列方程正确的是( )
A.2×1000(26﹣x)=800x B.1000(13﹣x)=800x
C.1000(26﹣x)=2×800x D.1000(26﹣x)=800x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
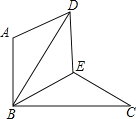
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年5月22日10时5分,西藏日咯则市定日县发生5.3级地震,该县部分地区受灾严重,我解放军某部火速向灾区救援,最初坐车以某一速度匀速前进,中途由于道路出现泥石流,被阻停下,耽误了一段时间,为了尽快赶到灾区救援,官兵们下车急行军匀速步行前往,下列是官兵们离出发地的距离S(千米)与行进时间t(小时)的函数大致图象,你认为正确的是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB的垂直平分线MN交AB于点E,交AC于点D,且AC=15cm,△BCD的周长等于25cm.

(1)求BC的长;
(2)若∠A=36°,并且AB=AC,求证:BC=BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副直角三角板叠放如图所示,现将含45°角的三角板ADE固定不动,把含30°角的三角板ABC绕顶点A顺时针旋转∠α(α=∠BAD且0°<α<180°),使两块三角板至少有一组边平行.
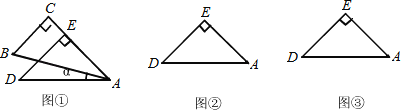
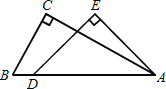
(1)如图①,α= °时,BC∥DE;
(2)请你分别在图②、图③的指定框内,各画一种符合要求的图形,标出α,并完成各项填空:图②中α= °时, ∥ ;图③中α= °时, ∥ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com