Question

【题目】如图，在四边形ABCD中，AD∥BC，∠C=90°，BC=CD=8，过点B作EB⊥AB，交CD于点E．若DE=6，则AD的长为（ ）

A．6 B．8 C．9 D．10

Answer 1

【答案】D

【解析】

试题分析：首先作BF⊥AD与点F，推得BF∥CD，判断出四边形BCDF是矩形；然后根据BC=CD=8，可得四边形BCDF是正方形，所以BF=BC；最后根据全等三角形的判定方法，证明△BCE≌△BAF，即可推得AF=CE，进而求出AD的长为多少即可．

如图，作BF⊥AD与点F，

，

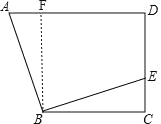∵BF⊥AD， ∴∠AFB=BFD=90°， ∵AD∥BC， ∴∠FBC=∠AFB=90°， ∵∠C=90°，

∴∠C=∠AFB=∠BFD=∠FBC=90°． ∴四边形BCDF是矩形． ∵BC=CD，∴四边形BCDF是正方形， ∴BC=BF=FD． ∵EB⊥AB， ∴∠ABE=90°， ∴∠ABE=∠FBC， ∴∠ABE﹣∠FBE=∠FBC﹣∠FBE， ∴∠CBE=∠FBA． 在△BAF和△BEC中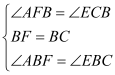， ， ∴△BAF≌△BEC， ∴AF=EC． ∵CD=BC=8，DE=6， ∴DF=8，EC=2， ∴AF=2， ∴AD=8+2=10．