
����Ŀ��ѧУΪ�˽���꼶ѧ����������������������������Ը��꼶��500��ͬѧ�����ʾ����ԣ��������ȡ��10��ͬѧ���ʾ���ͳ�Ƴɼ����£�
�÷� | 10 | 9 | 8 | 7 | 6 |
���� | 3 | 3 | 2 | 1 | 1 |
��1��������10��ͬѧ��β��Ե�ƽ���÷֣�
��2������÷ֲ�����9�ֵĶ���Ϊ���������������� 500��ѧ����������������������������������
��3��С�����ڰ༶����40�ˣ�����ȫ���μ�����β��ԣ�ƽ����Ϊ7.8�֣�С���IJ��Գɼ���8�֣�С��˵���ҵIJ��Գɼ��ڰ༶�е�ƫ�ϣ���ͬ�����Ĺ۵���Ϊʲô��
���𰸡���1��8.6����2��300����3����ͬ�⣬���ɼ�����.
��������
��1�����ݼ�Ȩƽ�����ļ��㹫ʽ��ƽ��������2�����ݱ������������10��ͬѧ��������ռ�ı�����Ȼ������500��ѧ���ж���������������������������������3������ƽ��������λ����������з���˵������.
�⣺��1��![]()
����10��ͬѧ��β��Ե�ƽ���÷�Ϊ8.6�֣�
��2��![]() ���ˣ�
���ˣ�
���� 500��ѧ��������������������������������Ϊ300�ˣ�
��3����ͬ��
ƽ���������ܼ���ֵ��Ӱ�죬����С���IJ��Գɼ�Ϊ8�֣�����һ���������ijɼ��ڰ༶�е�ƫ�ϣ�Ҫ��֪���Լ��ijɼ��Ƿ����е�ƫ�ϣ���Ҫ�˽����ѧ���ɼ�����λ��.


 ��ʦ������Ԫ��ĩ���100��ϵ�д�
��ʦ������Ԫ��ĩ���100��ϵ�д� ��У������Ԫͬ��ѵ��������ϵ�д�
��У������Ԫͬ��ѵ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
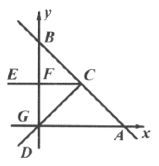
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() ��x�ύ�ڵ�A,��y�ύ�ڵ�B,��C��AB���е㣬��ECD�Ƶ�C��˳ʱ����ת���ҡ�ECD=45��,��ECD��һ��CE��y���ڵ�F,��ʼʱ��һ��CD������O,��G����Ϊ��-2,0),����ECD��ת�����У�����CD��x��Ľ����ɵ�O����G�Ĺ����У�����B��C��F�����Բ��Բ����������·����Ϊ�� ��
��x�ύ�ڵ�A,��y�ύ�ڵ�B,��C��AB���е㣬��ECD�Ƶ�C��˳ʱ����ת���ҡ�ECD=45��,��ECD��һ��CE��y���ڵ�F,��ʼʱ��һ��CD������O,��G����Ϊ��-2,0),����ECD��ת�����У�����CD��x��Ľ����ɵ�O����G�Ĺ����У�����B��C��F�����Բ��Բ����������·����Ϊ�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
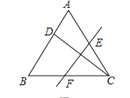
����Ŀ����ͼ����֪D�ǵȱߡ�ABC��AB�ϵ�һ�㣬�ֽ���ABC�۵���ʹ��C��D�غϣ��ۺ�ΪEF����E��F�ֱ���AC��BC�ϣ����AD��DB=1��2����CE��CF��ֵΪ____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������aʹ����x�ķ�ʽ����![]() ��2�������⣬��ʹ����x�IJ���ʽ��
��2�������⣬��ʹ����x�IJ���ʽ��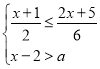 ������4�������⣬��������������������a�ĺ��ǣ�������
������4�������⣬��������������������a�ĺ��ǣ�������
A.��14B.��17C.��20D.��23
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ���ı���ABCD�У���E��AD���ϵĵ㣬����BE��
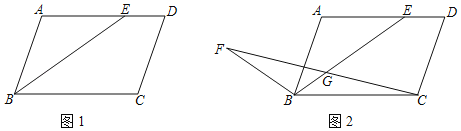
��1����ͼ1����BEƽ�֡�ABC��BC��8��ED��3����ƽ���ı���ABCD���ܳ���
��2����ͼ2����F��ƽ���ı�����һ�㣬FB��CD������BF��CF��CF��BE�ཻ�ڵ�G������FBE+��ABC��180������G��CF���е㣬��֤��2BG+ED��BC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y��ax2��bx��c��a��0��a��b��cΪ��������ͼ����A����1��0����B��0��2����
��1��b�� ���ú���a�Ĵ���ʽ��ʾ����c�� ��
��2����O������ԭ�㣬��C�Ǹú���ͼ��Ķ��㣬����AOC�����Ϊ1����a�� ��
��3����x��1ʱ��y��5�����ͼ��ֱ��д��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y��ax2��bx��c��a��0���У�����y���Ա���x�IJ��ֶ�Ӧֵ���±���

��1����ö��κ����ı���ʽ��
��2���ö��κ���ͼ�����x��ԳƵ�ͼ������Ӧ�ĺ�������ʽ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC�ǵ���ֱ�������Σ���BAC��90��������ABC�Ƶ�C˳ʱ�뷽����ת�õ���A��B��C������ת��Ϊ������90��������180��ʱ����A��D��AC������ΪD��A��D��B��C���ڵ�E��
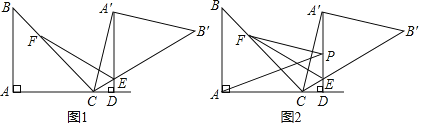
��1����ͼ1������CA��D��15��ʱ������A��EC��ƽ����EF��BC�ڵ�F��
��д����ת�����Ķ�����
����֤��EA��+EC��EF��
��2����ͼ2���ڣ�1���������£���P��ֱ��A��D�ϵ�һ�����㣬����PA��PF����AB��![]() �����߶�PA+PF����Сֵ��������������ţ�
�����߶�PA+PF����Сֵ��������������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
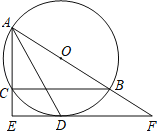
����Ŀ����ͼ����O����ABC�����Բ��ABΪֱ������BAC��ƽ���߽���O�ڵ�D������D��DE��AC�ֱ�AC���ӳ����ڵ�E����AB���ӳ����ڵ�F��
��1����֤��EF�ǡ�O�����ߣ�
��2����AC��8��CE��4����BD�ij����������������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com