
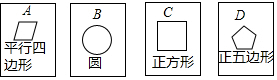
分析 (1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果;
(2)由树状图可求得摸出两张牌面图形既是轴对称图形又是中心对称图形的情况,再利用概率公式即可求得答案.
解答 解:(1)画树状图得: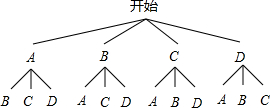
则共有12种等可能的结果;
(2)∵既是轴对称图形又是中心对称图形的只有B、C,
∴既是轴对称图形又是中心对称图形的有2种情况,
∴既是轴对称图形又是中心对称图形的概率为$\frac{2}{12}$=$\frac{1}{6}$.
点评 本题考查的是用列表法或画树状图法求概率.列表法或画树状图法可以不重复不遗漏的列出所有可能的结果,列表法适合于两步完成的事件,树状图法适合两步或两步以上完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,Rt△AOB的斜边OA在x轴的正半轴上,∠OBA=90°,且tan∠AOB=$\frac{1}{2}$,OB=2$\sqrt{5}$,反比例函数y=$\frac{k}{x}$的图象经过点B.
如图,在平面直角坐标系中,Rt△AOB的斜边OA在x轴的正半轴上,∠OBA=90°,且tan∠AOB=$\frac{1}{2}$,OB=2$\sqrt{5}$,反比例函数y=$\frac{k}{x}$的图象经过点B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
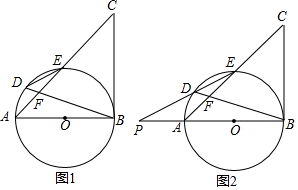
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
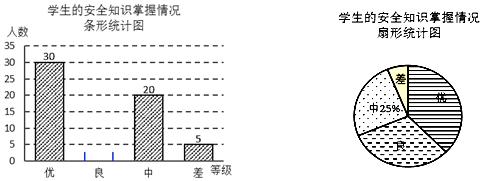
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
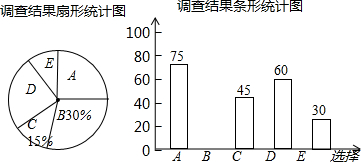
| 造成医患关系紧张的原因(单选) A.药价高 B.检测项目太多且收费太高 C.住院报销比例低 D.医疗费与个人收入不相称 E.其他 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校1200名学生参加了全市组织的“经典诵读”活动,该校随机选取部分学生,对他们在三、四两个月的诵读时间进行调查,下面是根据调查数据制作的统计图表的一部分,三月日人均诵读时间的频数分布直方图.
某校1200名学生参加了全市组织的“经典诵读”活动,该校随机选取部分学生,对他们在三、四两个月的诵读时间进行调查,下面是根据调查数据制作的统计图表的一部分,三月日人均诵读时间的频数分布直方图.| 日人均诵读时间x/h | 人数 | 百分比 |
| 0≤x≤0.5 | 6 | |
| 0.5<x≤1 | 30 | |
| 1<x≤1.5 | 50% | |
| 1.5<x≤2 | 10 | 10% |
| 2<x≤2.5 | b | c |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com