
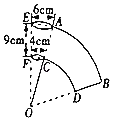
【题目】如图所示是一个纸杯,它的母线延长后形成的立体图形是圆锥,该圆锥的侧面展开图是扇形OAB,经测量,纸杯开口圆的直径为6cm,下底面直径为4![]() ,母线长EF=9cm,求扇形OAB的圆心角及这个纸杯的表面积.(结果保留根号和π)
,母线长EF=9cm,求扇形OAB的圆心角及这个纸杯的表面积.(结果保留根号和π)
【答案】40度 49π![]()
【解析】
(1)设∠AOB=n°,AO=R,则CO=R-9,利用圆锥的侧面展开图扇形的弧长等于圆锥底面周长作为相等关系列方程,并联立成方程组求解即可;
(2)求纸杯的侧面积即为扇环的面积,需要用大扇形的面积减去小扇形的面积.纸杯表面积=S纸杯侧面积+S纸杯底面积.
解:由题意可知:![]() =6πcm,
=6πcm, ![]() =4π,设∠AOB=n,AO=R,则CO=R﹣9, 由弧长公式得:l=
=4π,设∠AOB=n,AO=R,则CO=R﹣9, 由弧长公式得:l=![]() ,
,
∴![]() ,
,
解得:n=40,R=27,
故扇形OAB的圆心角是40度.
∵R=27,R﹣9=18,
∴S扇形OCD= ![]() ×4π×18=36π(cm2),
×4π×18=36π(cm2),
S扇形OAB= ![]() ×6π×27=81π(cm2),
×6π×27=81π(cm2),
纸杯侧面积=S扇形OAB﹣S扇形OCD=81π﹣36π=45π(cm2),
纸杯底面积=π22=4π(cm2)
纸杯表面积=45π+4π=49π(cm2).


科目:初中数学 来源: 题型:
【题目】市政规划出一块矩形土地用于某项目开发,其中![]()
![]() ,设计分区如图所示,
,设计分区如图所示,![]() 为矩形内一点,作
为矩形内一点,作![]() 于点
于点![]() 交
交![]() 于点
于点![]() ,
,![]() 过点
过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,其中丙区域用于主建筑区,其余各区域均用于不同种类绿化.
,其中丙区域用于主建筑区,其余各区域均用于不同种类绿化.
![]() 若点
若点![]() 是
是![]() 的中点,求
的中点,求![]() 的长;
的长;
![]() 要求绿化占地面积不小于
要求绿化占地面积不小于![]() ,规定乙区域面积为
,规定乙区域面积为![]()
①若将甲区域设计成正方形形状,能否达到设计绿化要求?请说明理由;
②若主建筑丙区域不低于乙区域面积的![]() ,则
,则![]() 的最大值为
的最大值为 ![]() (请直接写出答案)
(请直接写出答案)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 分别表示两名同学沿着同一路线运动的一次函数图象,图中
分别表示两名同学沿着同一路线运动的一次函数图象,图中![]() 和
和![]() 分别表示运动路程和时间,已知甲的速度比乙快.有下列结论:
分别表示运动路程和时间,已知甲的速度比乙快.有下列结论:
①射线![]() 表示甲的运动路程与时间的函数关系
表示甲的运动路程与时间的函数关系
②甲出发时,乙已经在甲前面12米;
③8秒后,甲超过了乙;
④64秒时,甲追上了乙
其中,正确结论的个数是( )
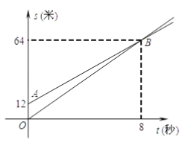
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
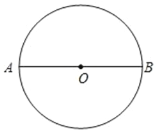
【题目】⊙O 的直径 AB 长为 10,弦 MN⊥AB,将⊙O 沿 MN 翻折,翻折后点 B 的对应点为点 B′,若 AB′=2,MB′的长为( )
A. 2 ![]() B. 2
B. 2![]() 或 2
或 2![]() C. 2
C. 2![]() D. 2
D. 2 ![]() 或 2
或 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
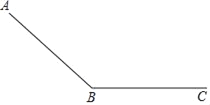
【题目】如图,一个滑道由滑坡(AB段)和缓冲带(BC段)组成,滑雪者在滑坡上滑行的距离y1(单位:m)和滑行时间t1(单位s)满足二次函数关系,并测得相关数据:
滑行时间t1/s | 0 | 1 | 2 | 3 | 4 |
滑行距离y1/s | 0 | 4.5 | 14 | 28.5 | 48 |
滑雪者在缓冲带上滑行的距离y2(单位:m)和滑行时间t2(单位:s)满足:y2=52t2﹣2t22,滑雪者从A出发在缓冲带BC上停止,一共用了23s.
(1)求y1和t1满足的二次函数解析式;
(2)求滑坡AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,![]() 的三个顶点在坐标轴上,
的三个顶点在坐标轴上,![]() ,且
,且![]() ,将
,将![]() 沿着
沿着![]() 翻折到
翻折到![]() .
.

(1)求点![]() 的坐标;
的坐标;
(2)动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 轴以
轴以![]() 个单位秒的速度向终点
个单位秒的速度向终点![]() 运动,过点
运动,过点![]() 作直线
作直线![]() 垂直于
垂直于![]() 轴,分别交直线
轴,分别交直线![]() 、直线
、直线![]() 于点
于点![]() 、
、![]() ,设线段
,设线段![]() 的长为
的长为![]() ,点
,点![]() 运动时间为
运动时间为![]() 秒,求
秒,求![]() 与
与![]() 的关系式,并写出
的关系式,并写出![]() 的取值范围.
的取值范围.
(3如图2在(2)的条件下,点![]() 为点
为点![]() 关于
关于![]() 轴的对称点,点
轴的对称点,点![]() 在直线
在直线![]() 上,是否存在点
上,是否存在点![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形;若存在,求出
为顶点的四边形为平行四边形;若存在,求出![]() 值和点
值和点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
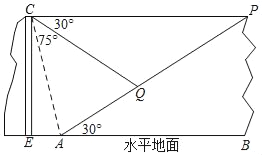
【题目】如图,某地质公园中有两座相邻小山.游客需从左侧小山山脚E处乘坐竖直观光电梯上行100米到达山顶C处,然后既可以沿水平观光桥步行到景点P处,也可以通过滑行索道到达景点Q处,在山顶C处观测坡底A的俯角为75°,观测Q处的俯角为30°,已知右侧小山的坡角为30°(图中的点C,E,A,B,P,Q均在同一平面内,点A,Q,P在同一直线上)
(1)求∠CAP的度数及CP的长度;
(2)求P,Q两点之间的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接:“国家卫生城市”复检,某市环卫局准备购买A,B两种型号的垃圾箱,通过市场调研得知:购买3个A型垃圾箱和2个B型垃圾箱共需540元,购买2个A型垃圾箱比购买3个B型垃圾箱少用160元.
(1)求每个A型垃圾箱和B型垃圾箱各多少元?
(2)该市现需要购买A,B两种型号的垃圾箱共30个,其中买A型垃圾箱不超过16个.
①求购买垃圾箱的总花费w(元)与A型垃圾箱x(个)之间的函数关系式;
②当买A型垃圾箱多少个时总费用最少,最少费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com