
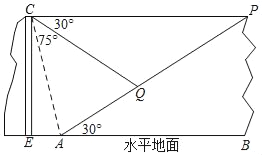
����Ŀ����ͼ��ij���ʹ�������������Сɽ���ο�������Сɽɽ��E��������ֱ�۹��������100����ɽ��C����Ȼ��ȿ�����ˮƽ�۹��Ų��е�����P����Ҳ����ͨ�������������ᄚ��Q������ɽ��C���۲��µ�A�ĸ���Ϊ75�㣬�۲�Q���ĸ���Ϊ30�㣬��֪�Ҳ�Сɽ���½�Ϊ30�㣨ͼ�еĵ�C��E��A��B��P��Q����ͬһƽ���ڣ���A��Q��P��ͬһֱ���ϣ�
��1�����CAP�Ķ�����CP�ij��ȣ�
��2����P��Q����֮��ľ��룮������������ţ�
���𰸡���1��75�㣬200��2��![]()
��������
��1������ƽ���ߵ����ʵõ���APC����PAB��30�������������ε��ڽǺ͵õ���CAP��180�㩁75�㩁30�㣽75�������ݵ��������ε��ж������õ�PC��AP����P��PF��AB��F������ֱ�������ε����ʼ��ɵõ����ۣ���2�����ݵ��������ε��ж������õ�CQ��PQ����Q��QH��PC��H������ֱ�������ε����ʼ��ɵõ����ۣ�
��1����PC��AB��
���APC����PAB��30�㣬
���CAP��180�㩁75�㩁30�㣽75�㣬
���CAP����PCA��
��PC��AP��
��P��PF��AB��F��
��PF��CE��100��
��PA��2PF��200�ף�
��2���ߡ�PCQ����QPC��30�㣬
��CQ��PQ��
��Q��QH��PC��H��
��PH��![]() PC��100��
PC��100��
��PQ��![]() �ף�
�ף�
��P��Q����֮��ľ�����![]() �ף�
�ף�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijˮ���������أ�ij�찲��30�����˲�ժ���˻��ݮ��ÿ������ֻ��������һ�����������ÿ��ÿ��ժ0.4�����˻�0.3�ֲ�ݮ������������ۼ�ÿ��2000Ԫ����ݮ�ۼ�ÿ��3000Ԫ���谲������x�����˲�ժ���ˣ�����ˮ������ȫ���۳��������ܶ��yԪ��
��1����y��x֮��ĺ�����ϵʽ��
��2����Ҫ�����ժ���˵����������ڲ�ݮ���������������ܶ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������8����һ�������Ŀڴ���װ��2����������Ϊ����1������2����1������1��������Щ�����ɫ�ⶼ��ͬ������ҡ�ȣ�
��1��������������1����ǡ����������ĸ����� ��
��2���ȴ�����������1�����ٴ����µ�3��������������1���������оٷ�������״ͼ���б��������ζ���������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
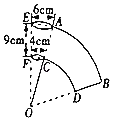
����Ŀ����ͼ��ʾ��һ��ֽ��������ĸ���ӳ����γɵ�����ͼ����Բ����Բ�IJ���չ��ͼ������OAB����������ֽ������Բ��ֱ��Ϊ6cm���µ���ֱ��Ϊ4![]() ��ĸ�߳�EF=9cm��������OAB��Բ�ĽǼ����ֽ���ı������������������źͦУ�
��ĸ�߳�EF=9cm��������OAB��Բ�ĽǼ����ֽ���ı������������������źͦУ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
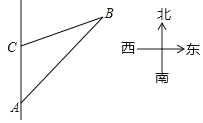
����Ŀ��һ�һ�����36km/h���ٶ��ں����������������У�����ʻ��A��ʱ�����ֱ�ƫ��37�㷽����һ������B�����ּ�������20���Ӻ�C�������ֵ���B�����ı�ƫ��67�㷽�����ʱ���������B�ľ���Ϊ_____km���������ȷ��0.1���ο����ݣ�sin37���0.6��cos37���0.8��tan37���0.75��sin67���0.920��cos67���0.391��tan67���2.356��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
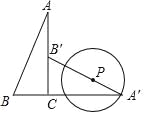
����Ŀ����ͼ����ABC�У���ACB=90�㣬tanA=![]() ��AB=13������ABC�Ƶ�C˳ʱ����ת90��õ���A'B'C��PΪ�߶�A��B���ϵĶ��㣬�Ե�PΪԲ�ģ�PA�䳤Ϊ�뾶����P������P���ABC�ı�����ʱ����P�İ뾶Ϊ_____��
��AB=13������ABC�Ƶ�C˳ʱ����ת90��õ���A'B'C��PΪ�߶�A��B���ϵĶ��㣬�Ե�PΪԲ�ģ�PA�䳤Ϊ�뾶����P������P���ABC�ı�����ʱ����P�İ뾶Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,ԣ����ѧ����ѵ���У�һʵ�����б��O�㴦�׳�,����׳�·�߿����ö��κ���![]() �̻�,б�¿�����һ�κ���
�̻�,б�¿�����һ�κ���![]() �̻�,ʵ��������A�������ǣ�
�̻�,ʵ��������A�������ǣ�![]() ��.
��.
(1)����κ�������ʽ�Ͷ��κ���ͼ�����ߵ�P�����ꣻ
(2)���������ߵ���ߵ�P���O��A�á�POA�����POA�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
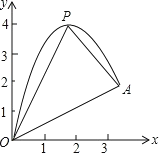
����Ŀ����ͼ��ʾ���ı���ABCD�����Σ���BC��x���ϣ���A��0��4������B��3��0����˫����y=![]() ��ֱ��BD���ڵ�D����E��
��ֱ��BD���ڵ�D����E��
��1����k��ֵ��
��2����ֱ��BD�Ľ���ʽ��
��3������CDE�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
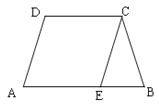
����Ŀ����������ABCD�У�AB��DC��AD��BC��CD����EΪAB��һ�㣬����CE��������һ������Ϊ���ʵ����� ��ʹ�ı���AECDΪ���Σ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com