
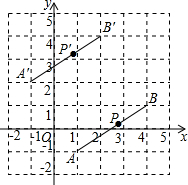
 如图,在平面直角坐标系中,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上,则这四个点组成的四边形ABB′A′的面积是( )
如图,在平面直角坐标系中,线段AB经过平移得到线段A′B′,其中点A,B的对应点分别为点A′,B′,这四个点都在格点上,则这四个点组成的四边形ABB′A′的面积是( )| A. | 4 | B. | 6 | C. | 9 | D. | 13 |
分析 首先根据平移的性质得出AB∥A′B′,且AB=A′B′,那么四边形ABB′A′是平行四边形,再利用勾股定理求出AB=BB′,那么?ABB′A′是正方形,根据正方形的面积公式即可求解.
解答 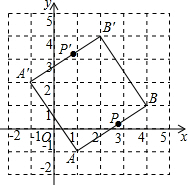 解:∵线段AB经过平移得到线段A′B′,
解:∵线段AB经过平移得到线段A′B′,
∴AB∥A′B′,且AB=A′B′,
∴四边形ABB′A′是平行四边形,
∵AB=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,BB′=$\sqrt{{3}^{2}+{2}^{2}}$=$\sqrt{13}$,
∴AB=BB′,
∴?ABB′A′是正方形,
∴四边形ABB′A′的面积=AB2=13.
故选D.
点评 本题考查了坐标与图形变化-平移,平移的性质,正方形的判定与性质,证明四边形ABB′A′是正方形是解题的关键.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:解答题
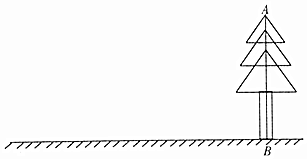 某个阳光明媚的一天,数学兴趣小组的同学们去测量一棵树AB的高度(这棵树底部可以到达,顶部不易到达),他们带的测量工具是:皮尺,标杆,小平面镜.请你帮他们完成以下问题.
某个阳光明媚的一天,数学兴趣小组的同学们去测量一棵树AB的高度(这棵树底部可以到达,顶部不易到达),他们带的测量工具是:皮尺,标杆,小平面镜.请你帮他们完成以下问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥-1 | B. | x>2 | C. | x≠2 | D. | x≥-1且x≠2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com